Resolução da prova de Raciocínio Lógico para Técnico do TST – TJAA
A prova de raciocínio lógico matemático do concurso para técnico judiciário Tribunal Superior do Trabalho, organizado pela FCC, cobriu de forma geral todos os temas do edital, sem que haja concentração em torno de um tema específico.

Vamos aos (didáticos) comentários:
As questões formuladas foram bem clássicas e tradicionais em provas de RLM: nesse quesito a banca não inovou.
Em relação à dificuldade empregada, foi uma prova simples, com nível intermediário de dificuldade com estruturas de questões que já foram abordadas pela própria FCC e por que não dizer, por outras bancas.
Vamos ao que interessa: análise das questões da prova do concurso do TST…
Resolução da prova de Raciocínio Lógico Técnico TST
Questão 16:
(FCC – 2017 – TST) O código de um sistema de classificação de processos é composto por três vogais juntas, seguidas por três algarismos. A ordenação começa com o 1º processo, cujo código é AAA000, e termina com o 125.000º processo, cujo código é UUU999, seguindo sempre a ordem alfabética das letras e ordem crescente do número composto pelos três algarismos. Nesse sistema de classificação, o 10.500º processo terá o código
Solução:
Esta questão mesclou, de forma direta, dois assuntos muito abordados pela Fundação Carlos Cagas: princípios combinatórios e padrões sequenciais. Vamos começar analisando as posições representadas por algarismos do sistema de classificação de processos (como se estivéssemos fixando as três vogais):
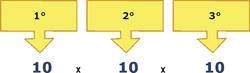
Ou seja, são 1000 codificações diferentes obtidas ao fixarmos uma mesma sequência de vogais. Para determinar o código do 10.500º processo, precisamos identificar o 11º termo da sequência AAA, AAE, AAI, … Como são poucos termos e a lógica de formação é relativamente simples, vamos escrever até encontramos o que procuramos:

Para escrever 500 números, a partir 0, teríamos que parar no número 499. Portanto, o 10500º código é AIA499.
Gabarito: Alternativa C.
Questão 17:
(FCC – 2017 – TST) Algumas cadeiras novas foram distribuídas por quatro andares de um edifício comercial. O 1º andar recebeu metade do total de cadeiras. O 2º andar recebeu a terça parte do total de cadeiras que o 1º andar recebeu. O 3º andar recebeu dois quintos das cadeiras recebidas pelos dois andares abaixo. Por fim, o 4º andar recebeu as 16 cadeiras restantes. Em tais condições, o total de cadeiras distribuídas para os andares pares foi igual a
Solução:
Começaremos indicando por x o número de cadeiras novas distribuídas pelos quatro andares de um edifício comercial. O 1º andar recebeu metade do número de cadeiras, ou seja:
![]()
O 2º andar recebeu a terça parte do total de cadeiras que o 1º andar recebeu, ou seja, recebeu 1/3 da metade do total de cadeiras:
![]()
O 3º andar recebeu dois quintos das cadeiras recebidas pelos dois andares abaixo, ou seja, 2/5 da soma de (x/2) e (x/6):
![]()
Como o 4º andar recebeu 16 cadeiras, a soma do total de cadeiras recebidas por todos os andares é igual a x:
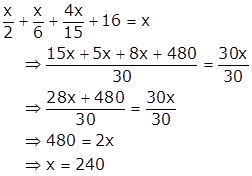
Portanto, o total de cadeiras distribuídas pelos andares pares foi:
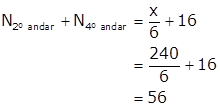
Gabarito: Alternativa A.
Questão 18:
(FCC – 2017 – TST) Maria, Nair, Olívia e Paula ganharam, juntas, na loteria e decidiram repartir o prêmio proporcionalmente ao valor desembolsado por cada uma no momento da aposta. Nair, que foi a que mais desembolsou dinheiro, deu o triplo do dinheiro dado por Paula, que foi a que menos desembolsou dinheiro. A soma do dinheiro desembolsado por Maria e Olívia foi 3/4 do dinheiro desembolsado por Nair. Sabendo-se que Paula recebeu R$ 12.000,00 de prêmio, o valor total do prêmio, recebido pelas quatro juntas, foi, em R$, de
- 000,00.
- 000,00.
- 000,00.
- 000,00.
- 000,00.
Solução:
Se Paula recebeu R$ 12.000 de prêmio, Nair recebeu o triplo desse valor, ou seja, R$ 36.000 (em função de proporcionalidade). Por outro lado, Maira e Olivia receberam 3/4 do prêmio recebido por Nair, ou seja, 3/4 de R$ 36.000. Esse valor é
![]()
As quatro receberam, juntas, o alor total de R$ 12.000 + R$ 36.000 + R$ 27.000 = R$ 75.000
Gabarito: Alternativa D.
Questão 19:
(FCC – 2017 – TST) O turno diário de trabalho de uma empresa é das 8h às 17h, de 2a a 6a feira, sendo que das 12h às 13h é o horário de almoço, não remunerado. Em determinada época do ano, os trabalhadores fizeram um acordo com a empresa para emendar o feriado de uma 5a feira com a 6a feira. O acordo previa que os funcionários estenderiam seu turno diário de trabalho em 15 minutos até completar a reposição das horas de trabalho do dia da emenda. Sabendo-se que o horário estendido teve início em uma 2a feira, dia 19 de junho, e que não houve outro feriado ou paralização até o último dia da compensação, então, o último dia da compensação foi
- 20 de junho.
- 28 de julho.
- 30 de junho.
- 31 de julho.
- 01 de agosto.
Solução:
Na carga-horária diária de trabalho constam 8h líquidas (sem levar em consideração o horário de almoço) e esse tempo é equivalente a 8 x 4 = 32 períodos de 15 minutos. Para emendar o feriado, os funcionários deverão compensar o equivalente a 32 dias (15 minutos/dia).
A seguir, vamos determinar quantos dias corridos que esse número de dias representa, observando que em cada semana são contados 5 dias úteis. Pois bem, dividindo 32 por 5, encontramos 6 (semanas) e 2 dias que não chegam a completar uma semana. Agora, considerando finais de semana, o tempo necessário, em dias, é
6 x 7 + 2 = 44 dias
Esses dias serão compensados entre os meses de junho, julho e agosto:
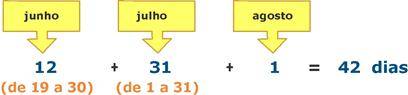
Gabarito: Alternativa D.
Questão 20:
(FCC – 2017 – TST) Considere como verdadeira a proposição: “Nenhum matemático é não dialético”. Laura enuncia que tal proposição implica, necessariamente, que
- se Carlos é matemático, então ele é dialético.
- se Pedro é dialético, então é matemático.
III. se Luiz não é dialético, então não é matemático.
- se Renato não é matemático, então não é dialético.
Das implicações enunciadas por Laura, estão corretas APENAS
- II e IV.
- I e III.
- I e II.
- III e IV.
- II e III.
Solução:
Esta é uma questão tradicional que envolve o que chamamos de diagramas lógicos. Podemos representar o conjunto de todas as pessoas como dialéticos ou não dialético e sabemos que esses conjuntos são complementares (não tem interseção e juntos determinam o universo de todos os elementos analisados).
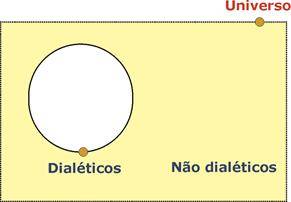
Se “Nenhum matemático é não dialético” concluímos que, caso existam matemáticos, esses estarão fora do conjunto dos não dialéticos (região amarela). Ou seja, estariam dentro do conjunto dos dialéticos (região branca). Na linguagem de conjuntos, o conjunto dos matemáticos estaria contido no conjunto dos dialéticos. Então:
- “se Carlos é matemático, então ele é dialético” é verdadeira.
- “se Pedro é dialético, então é matemático” é falsa.
- “se Luiz não é dialético, então não é matemático” é verdadeira.
- “se Renato não é matemático, então não é dialético” é falsa.
Gabarito: Alternativa B.
Questão 21:
Cássio, Ernesto, Geraldo, Álvaro e Jair são suspeitos de um crime. A polícia sabe que apenas um deles cometeu o crime. No interrogatório, os suspeitos deram as seguintes declarações:
Cássio: Jair é o culpado do crime.
Ernesto: Geraldo é o culpado do crime.
Geraldo: Foi Cássio quem cometeu o crime.
Álvaro: Ernesto não cometeu o crime.
Jair: Eu não cometi o crime.
Sabe-se que o culpado do crime disse a verdade na sua declaração. Dentre os outros quatro suspeitos, exatamente três mentiram na declaração. Sendo assim, o único inocente que declarou a verdade foi
a) Jair
b) Cássio.
c) Ernesto
d) Geraldo.
e) Álvaro.
Solução:
Em problemas dessa natureza, deveríamos testar todas as possibilidades possíveis (a quantidade de testes seria razoavelmente grande). Nosso primeiro teste levará em consideração que Cassio disse a Verdade (V). Ou seja, vamos supor que “Jair é o culpado do crime”. Partindo desse pressuposto, vamos analisar as cinco proposições:
| Cássio | Jair é o culpado do crime. | (V) |
| Ernesto | Geraldo é o culpado do crime. | (F) |
| Geraldo | Foi Cássio quem cometeu o crime. | (F) |
| Álvaro | Ernesto não cometeu o crime. | (V) |
| Jair | Eu não cometi o crime. | (F) |
Assim, o culpado (Jair) teria falado mentira e isso vai contra o que foi afirmado no enunciado. A seguir, vamos supor que Cassio tenha falado uma mentira. Ou seja, “Jair não é o culpado do crime”.
| Cássio | Jair é o culpado do crime. | (F) |
| Ernesto | Geraldo é o culpado do crime. | |
| Geraldo | Foi Cássio quem cometeu o crime. | |
| Álvaro | Ernesto não cometeu o crime. | |
| Jair | Eu não cometi o crime. | (V) |
Portanto, conclui-se que Jair é inocente e falou a verdade.
Gabarito: Alternativa A.
Questão 22:
(FCC – 2017 – TST) O total de P pessoas será distribuído em grupos com o mesmo número de integrantes, e sempre com o número máximo possível de integrantes. Se forem feitos 13 grupos, sobrarão 3 pessoas sem grupo. Se forem feitos grupos com 36 pessoas, sobrarão 11 pessoas sem grupo. Sendo P um inteiro maior do que zero, o menor valor possível de P é
Solução:
De forma geral, essa questão explora o conceito de divisão de números inteiros a partir do famoso Algoritmo de Euclides. De “Se forem feitos 13 grupos, sobrarão 3 pessoas sem grupo”, concluímos que o resto da divisão de P por 13 é 3.
![]()
Analogamente, de “Se forem feitos grupos com 36 pessoas, sobrarão 11 pessoas sem grupo”, concluímos que o resto da divisão de P por 36 seria 11, conforme indicamos a seguir:
![]()
Como o enunciado indaga pelo menor valor possível para P, vamos testar as alternativas, começando pela menor delas (existe um processo matemático formal para determinar P mas daria mais trabalho do que testar as alternativas). Dividindo 263 por 13 e por 36, obtemos:
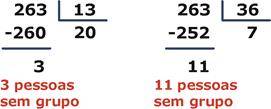
Ou seja, 263 atende às duas divisões das pessoas em grupos e é o menor valor dentre as alternativas. Portanto, a alternativa correta é a letra (A).
Gabarito: Alternativa A.
Terminamos!
Espero que estas palavras, um tanto extensas, possam elucidar dificuldades e erros cometidos.
Abraço,
Professor Marcelo Eustáquio



