Meus caros,

foi divulgado o caderno de questões e gabarito provisório do concurso do STJ, realizado no último domingo, dia 8 de abril.

Após análise das questões de raciocínio lógico-matemático (RLM), concluímos que não cabem recursos para anulação de itens ou alteração de gabaritos.

Vejam as questões:

Resolução da prova de Raciocínio Lógico
Superior Tribunal de Justiça:

Considere as proposições P e Q a seguir.

P: Todo processo que tramita no tribunal A ou é enviado para tramitar no tribunal B ou no tribunal C.

Q: Todo processo que tramita no tribunal C é enviado para tramitar no tribunal B.

A partir dessas proposições, julgue os itens seguintes.

Questão 22:

(CESPE – 2018 – STJ) Se um processo não tramita no tribunal C, então ele também não tramita no tribunal B.

Solução:

A partir da proposição Q, concluímos que o conjunto de todos os processos que tramitaram por C está contido no conjunto de todos os processos que tramitaram por B.

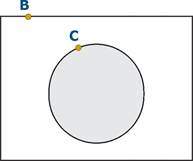
Assim, um processo que não tramitou em C poderia ter tramitado apenas em B, fazendo com que a assertiva apresentada esteja errada. A conclusão que poderíamos ter é que, caso um processo não tenha tramitado em B, ele também não teria tramitado em C.

Gabarito: Item ERRADO.

Questão 23:

(CESPE – 2018 – STJ) Se um processo for iniciado no tribunal A, então, com certeza, ele tramitará no tribunal B.

Solução:

A proposição P nos leva a concluir que os processos que tramitaram por A foram remetidos para B ou para C, porém sem tramitar simultaneamente nos dois tribunais. Logo, A está contido na união entre B e C.

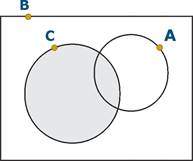
Porém, como C está contido em B, concluímos que A estará contido em B. Ou seja, todo processo originário de A tramitará por B, podendo ou não passar por C.

Gabarito: Item CORRETO.

Questão 24:

(CESPE – 2018 – STJ) 24 A proposição ¬P -> [P -> Q], em que ¬P denota a negação da proposição P, é uma tautologia, isto é, todos os elementos de sua tabela-verdade são V (verdadeiro).

Solução:

Usando as equivalências da lógica booleana (), temos:

Gabarito: Item CORRETO.

Questão 25:

(CESPE – 2018 – STJ) Se 10 processos que chegarem ao tribunal A em determinado dia forem separados de forma aleatória em dois grupos de 5 processos cada, um para ser encaminhado ao tribunal B, e outro, para o tribunal C, então essa separação poderá ser feita de, no máximo, 240 formas diferentes.

Solução:

O número de maneiras de direcionar 5 processos para B e 5 processos para C é equivalente a escolher 5 processos, de 10, para serem encaminhados para B e, dos restantes, escolher 5 para serem encaminhados para C. Logo, o número de escolhas será:

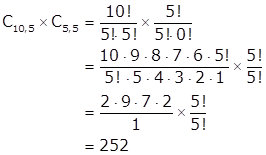
Gabarito: Item ERRADO.

E então, o que acharam? As questões foram fáceis?