Equivalência Lógica – Aula prática com questões comentadas

Olá meus amigos concurseiros! Vamos conversar sobre Equivalência Lógica?

Neste texto, vamos tratar das principais propriedades da lógica booleana cobradas em concursos e, assim, otimizar nosso tempo de estudo.

Para começar, costumo dizer que “equivalência lógica” está para a lógica assim como os “produtos notáveis” estão para a álgebra.

A priori, não temos a obrigação de conhecê-las, mas ao utilizá-las, deixamos de perder tempo na formulação das nossas resposta e ganhamos um ponto fácil.

1.     Equivalência lógica

Dizemos que duas proposições “p” e “q” são equivalentes se os resultados de suas tabelas-verdade são idênticos (ou seja, as colunas com os valores de p e q são iguais). Para dizer que “p” e “q” são equivalentes, escrevemos “p = q”. Um exemplo simples está na dupla negação, ~(~p), equivalente a p. Observe a tabela seguinte:

Enfim, proposições equivalentes é sinônimo de mesma sequência de valores na devida coluna da tabela verdade. Superada essa definição, vamos lembrar das principais equivalências que as provas de concurso trazem…

Equivalências lógicas básicas

O início da nossa lista contém equivalências diretas e intuitivas quando associadas a propriedades e equivalências usadas na própria álgebra. As duas primeiras, de certa forma, tratam de “redundâncias” no emprego de construções lógicas:

Suponha que P seja a proposição “Pedro é ótimo aluno”. Assim, a proposição composta “Pedro é ótimo aluno e Pedro é ótimo aluno” pode ser resumida em “P: Pedro é ótimo aluno”.

É um pouco (muito!) estranho pensar nesse tipo de construção, mas a lógica matemática possui ferramentas para tratá-las.

A ideia é a mesma que fora apresentada acima e agora a redundância está no uso do conectivo “ou” para duas proposições equivalentes. Assim, a proposição “Estudar RLM é desafiador ou Estudar RLM é desafiador” é equivalente a “Estudar RLM é desafiador”

Até o momento, nada de extraordinário. Nas duas equivalências a seguir, destacamos uma propriedade que diz que a ordem dos operandos (proposições) não altera o resultado quando se tratar de “conjunção” ou “disjunção”. Essa característica é chamada de comutatividade.

Aqui podemos traçar um paralelo entre a disjunção e a multiplicação de números reais. Assim como a ordem dos fatores não altera o produto (resultado da multiplicação), a ordem das proposições P e Q não altera a tabela-verdade da proposição P e Q.

Vejam:

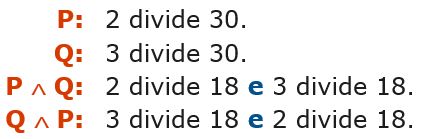
A  mensagem passada com as frases (P e Q) e (Q e P) é a mesma.

Para a disjunção, o paralelo que costumo traçar está relacionado à adição de números naturais. Da mesma forma que a ordem dos fatores não altera a adição (resultado da soma), a ordem das proposições P e Q não altera a tabela-verdade da proposição P ou Q. Veja que, mesmo alterando a ordem das proposições P e Q seguinte, a mensagem não tem significado modificado.

Equivalências de De Morgan

As importantíssimas relações de De Morgan tratam, em última análise, da negação de proposições lógicas compostas. Mais especificamente, da equivalência para a negação da conjunção e da equivalência para a disjunção de proposições simples:

Leia assim: “A negação da conjunção ~(P e Q) é equivalente à disjunção das negações (~P) ou (~Q)”. Vejam uma questão que explora essa equivalência lógica:

Exemplo 01.

(FCC – 2017 – TCE-SP) Uma afirmação que corresponda à negação lógica da afirmação “Pedro distribuiu amor e Pedro colheu felicidade” é:

(A) Pedro não distribuiu amor ou Pedro não colheu felicidade.
(B) Pedro distribuiu ódio e Pedro colheu infelicidade.
(C) Pedro não distribuiu amor e Pedro não colheu felicidade.
(D) Se Pedro colheu felicidade, então Pedro distribuiu amor.
(E) Pedro não distribuiu ódio e Pedro não colheu infelicidade.

Solução:

Questão clássica na qual buscamos proposição equivalente para a negação para “Pedro distribuiu amor e Pedro colheu felicidade”. Para negá-la, trocamos o conectivo por “ou” e negamos as proposições “Pedro distribuiu amor” e “Pedro colheu felicidade”. Vejam como fica:

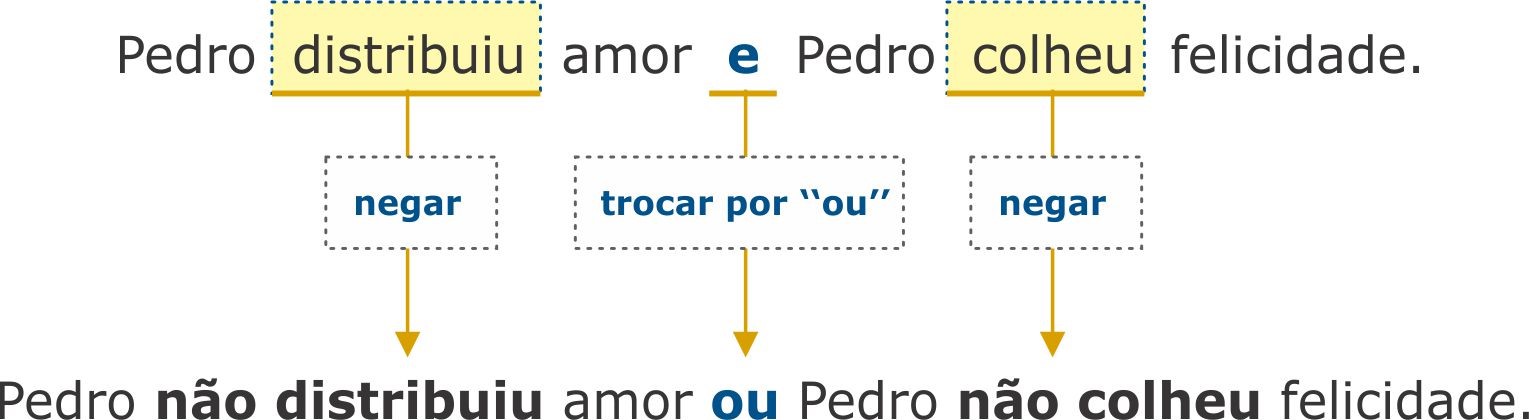
Gabarito: Alternativa A.

E então, o que acharam? Fácil ou difícil? Vamos para a 2ª equivalência de De Morgan: a negação da disjunção de duas proposições simples:

Leia assim: “A negação da disjunção ~(P Ú Q) é equivalente à disjunção das negações (~Q) Ù (~Q)”. Bem parecida com a anterior…

Exemplo 02.

(VUNESP – 2017 – TJSP) Uma negação lógica para a afirmação “João é rico, ou Maria é pobre” é:

(A) Se João é rico, então Maria é pobre.
(B) João não é rico, e Maria não é pobre.
(C) João é rico, e Maria não é pobre.
(D) Se João não é rico, então Maria não é pobre.
(E) João não é rico, ou Maria não é pobre.

Solução:

Nesta questão, a proposição a ser negada trata-se da disjunção de duas proposições lógicas simples. Para tal, trocamos o conectivo por “e” e negamos as proposições “João é rico” e “Maria é pobre”. Vejam como fica:

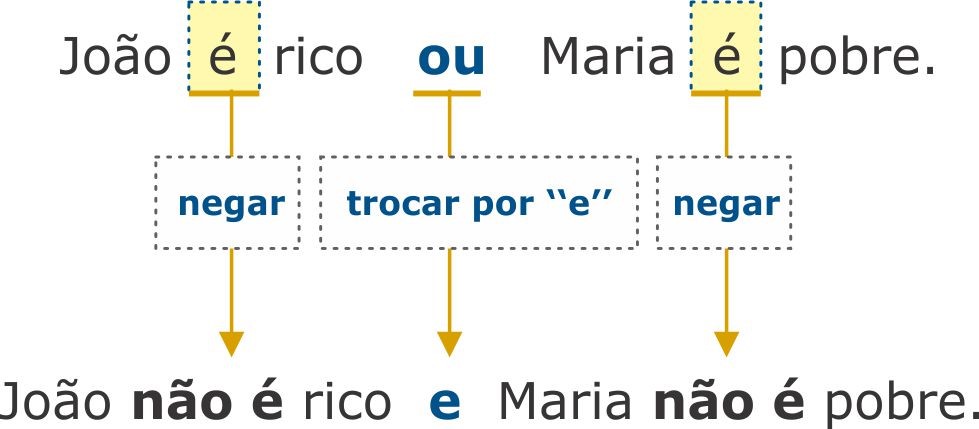
Gabarito: Alternativa B.

Equivalências da condicional

A maior parte das equivalências envolvem a proposição P -> Q, chamada de condicional na qual P e Q são, respectivamente, o antecedente e o consequente. Nomes a parte, a primeira equivalência diz respeito à transformação da condicional em uma disjunção:

Para confirmar, basta lembrar da tabela-verdade de P -> Q e construir a de ~P ou Q. Para a primeira, lembra que é falsa em apenas uma ocasião (P é verdadeira e Q falsa):

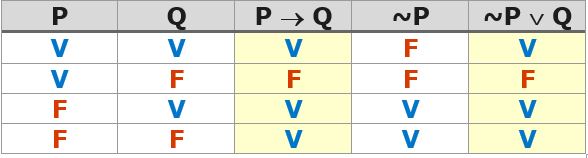
Ou seja, a equivalência é obtida a partir da disjunção entre a negação do antecedente (~P) e o consequente (Q). A seguir, observe como tal equivalência já foi cobrada:

Exemplo 03.

(IBFC – 2016 – EBSERH) De acordo com a lógica proposicional, a frase que é equivalente a: “Se Marcos estudou, então foi aprovado” é:

(A) Marcos não estudou e foi aprovado.
(B) Marcos não estudou e não foi aprovado.
(C) Marcos estudou ou não foi aprovado.
(D) Marcos estudou se, e somente se, foi aprovado.
(E) Marcos não estudou ou foi aprovado.

Solução:

Em “Se Marcos estudou, então foi aprovado”, antecedente e consequente são, respectivamente, dados dos “Marcos estudou” e “foi aprovado”. Para identificar a proposição equivalente, desconsideramos o “se”, negamos o antecedente, trocamos o “então” pelo “ou” e, por fim, mantemos o consequente:

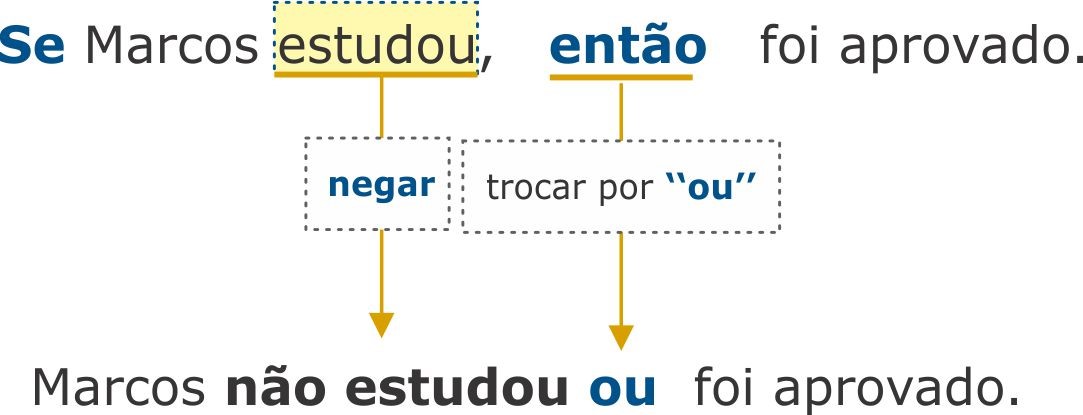
Gabarito: Alternativa E.

Da equivalência apresentada em (7) podemos deduzir outra propriedade que vem sendo muito cobrada recentemente. Para tal, basta trocar, em P -> Q = ~P ou Q, a proposição P pela sua negação. Veja:

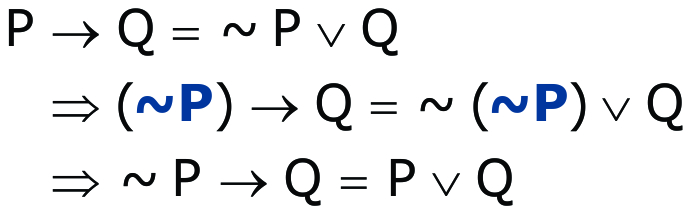
O uso é muito parecido com a propriedade (7): a disjunção pode se transformada em proposição condicional negando-se a primeira proposição, trocando o “ou” pelo “então”, mantendo a segunda proposição para, a seguir, fazer devidos ajustes. Vejam a próxima questão:

Exemplo 04.

(Quadrix – 2017 – CRF MT) A afirmação “Maria é médica ou João é professor” tem como sentença logicamente equivalente:

(A) Se João é professor, então Maria é médica.
(B) Se Maria é médica, então João é professor.
(C) Se Maria não é médica, então João é professor.
(D) Não é verdade que Maria é médica, então João é professor.
(E) Não é verdade que João é professor, então Maria é médica.

Solução:

Em “Se Marcos estudou, então foi aprovado”, antecedente e consequente são, respectivamente, dados dos “Marcos estudou” e “foi aprovado”. Para identificar a proposição equivalente, desconsideramos o “se”, negamos o antecedente, trocamos o “então” pelo “ou” e, por fim, mantemos o consequente:

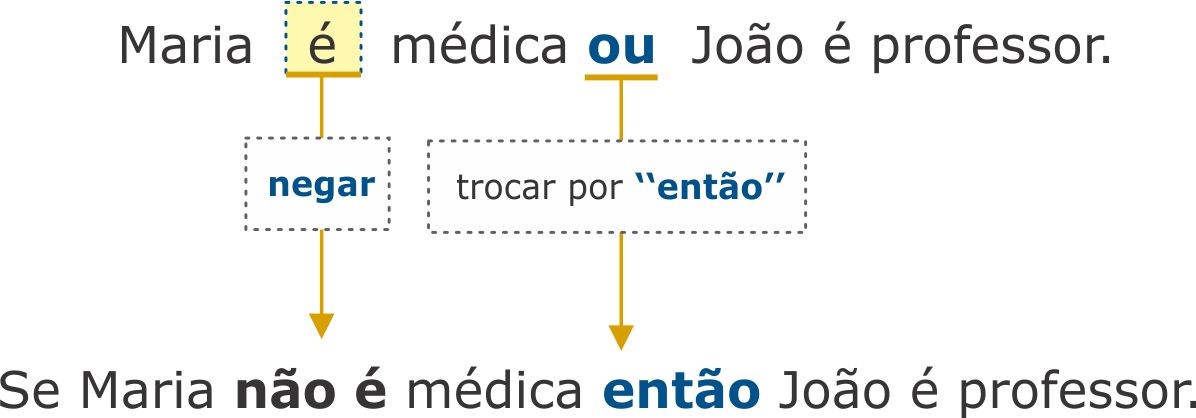
Gabarito: Alternativa C.

A maior parte das equivalências que compõem este texto envolve a proposição condicional e, para seguir para o final, vamos conversar sobre mais duas regrinhas bem importante: a “contra-positiva” e a negação da proposição condicional:

Esta equivalência, além de despencar em provas de concurso, é muito importante na própria matemática para propor demonstrações mais simples em certas situações. A ideia é partir da negação do consequente para desenvolver linha de raciocínio para chegar à negação do antecedente.

Exemplo 05.

(FCC – 2016 – TRT 20ª Região) Do ponto de vista da lógica, a proposição “se tem OAB, então é advogado” é equivalente à

(A) tem OAB ou é advogado.
(B) se não tem OAB, então não é advogado.
(C) se não é advogado, então não tem OAB.
(D) é advogado e não tem OAB.
(E) se é advogado, então tem OAB.

Solução:

Resolver esta questão consiste em aplicar a contra-positiva para determinar proposição equivalente para “se tem OAB, então é advogado”. Para tal, partimos da negação de “é advogado” para obter a negação de “tem OAB”. Ou seja:

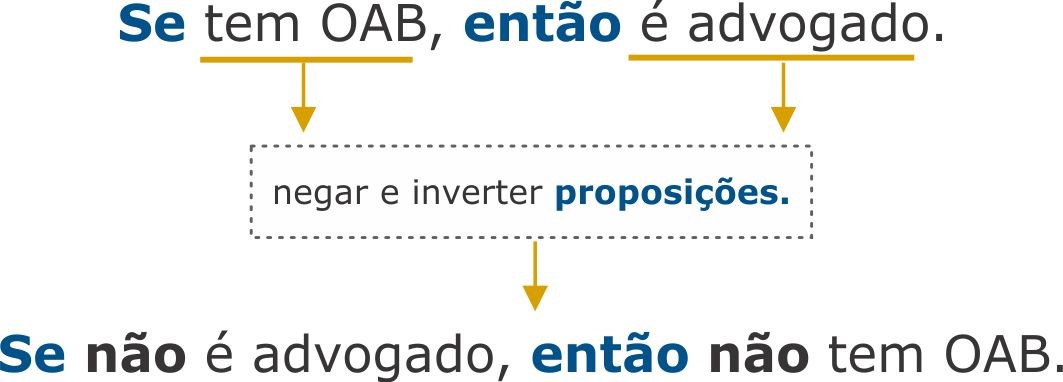
Gabarito: Alternativa C.

Para encerrar nossa sequência de propriedades e equivalências, vamos deduzir a negação da proposição condicional usando mecanismo mais “algébrico”. Para tal, substituímos P -> Q = ~P ou Q para, a seguir, usar a relação de De Morgan:

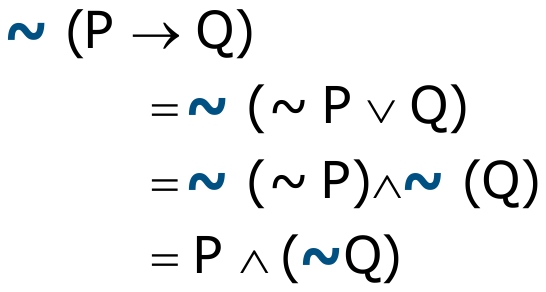
Resumido: para negar P -> Q, partimos do mesmo ponto (P) e chegamos a resultado diferente (~Q). Ou seja, repetimos os mesmos passos, mas chegamos a lugar diferente do anterior.

Exemplo 06.

(FUNCAB – 2016 – ANS) A negação de afirmação condicional “Se o beneficiário estiver acima do peso, ele é sedentário” é:

(A) o beneficiário não está acima do peso e ele é sedentário.
(B) se o beneficiário não estiver acima do peso, ele é sedentário.
(C) o beneficiário não está acima do peso e ele não é sedentário.
(D) o beneficiário está acima do peso e ele não é sedentário.
(E) se o beneficiário estiver acima do peso, ele não é sedentário.

Solução:

A negação da proposição procurada envolve em partir do mesmo ponto (o beneficiário estiver acima do peso) e chegar a resultado diverso do inicialmente considerado (ele não é sedentário).

Perceba que a negação da proposição condicional é obtida após seguir alguns passos: desconsiderar o “se”, manter antecedente, trocar “então” pelo conectivo “e” e, por fim, negar consequente.

Gabarito: Alternativa D.

Exemplo 07.

(CESPE – 2016 – Polícia Científica PE) Considere as seguintes proposições para responder a questão.

P1: Se há investigação ou o suspeito é flagrado cometendo delito, então há punição de criminosos.

Assinale a opção que apresenta uma negação correta da proposição P1.

(A) Se não há punição de criminosos, então não há investigação ou o suspeito não é flagrado cometendo delito.
(B) Há punição de criminosos, mas não há investigação nem o suspeito é flagrado cometendo delito.
(C) Há investigação ou o suspeito é flagrado cometendo delito, mas não há punição de criminosos.
(D) Se não há investigação ou o suspeito não é flagrado cometendo delito, então não há punição de criminosos.
(E) Se não há investigação e o suspeito não é flagrado cometendo delito, então não há punição de criminosos.

Solução:

P1 é uma proposição condicional na qual o antecedente é “há investigação ou o suspeito é flagrado cometendo delito” e o consequente é “há punição de criminosos”. Para negá-la, vamos transformá-la em conjunção (com o uso do conectivo “e” no lugar do “então”), repetindo o antecedente e negando o consequente. Obtemos:

~P1: Se há investigação ou o suspeito é flagrado cometendo delito
e não há punição de criminosos.

        Um pequeno ajuste foi feito, sem prejuízo para o significado de ~P1: “e não há” e “mas não há” são sinônimos.

Gabarito: Alternativa C.

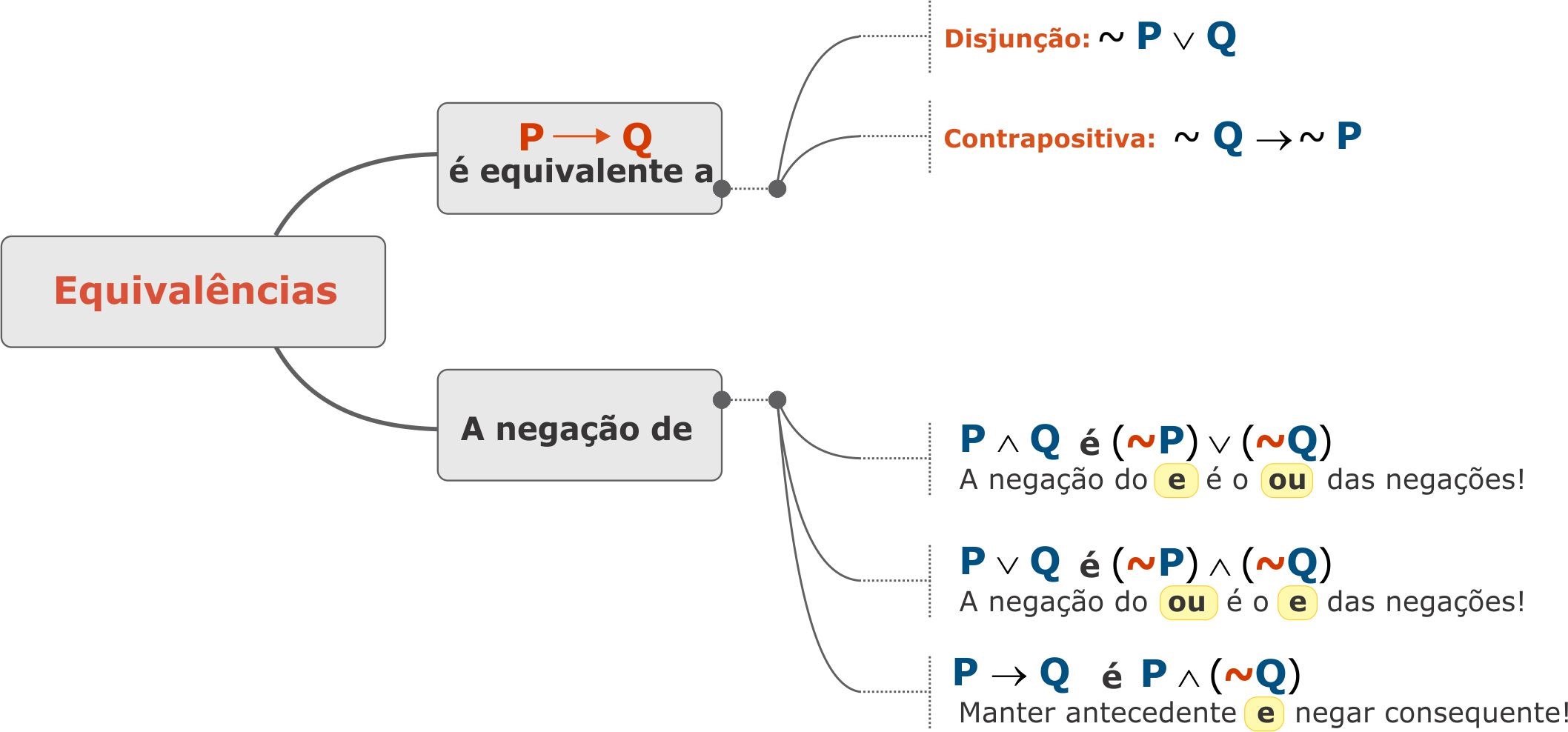
2. Resumindo…

Quais são as principais equivalências lógicas para guardar para a hora da prova? A resposta está no mapa mental seguinte:

3. Vamos praticar…

Q01 (FCC – 2017 – TC-SP) Assinale a alternativa que apresenta uma afirmação equivalente à afirmação “Se comprei e paguei, então levei”.

(A) Se comprei e não paguei, então não levei.
(B) Se não comprei e paguei, então não levei.
(C) Se não levei, então não paguei ou não comprei.
(D) Se comprei ou paguei, então não levei.
(E) Se levei, então comprei e paguei.

Q02 (CESPE – 2017 – TRF 1ª Região) Em uma reunião de colegiado, após a aprovação de uma matéria polêmica pelo placar de 6 votos a favor e 5 contra, um dos 11 presentes fez a seguinte afirmação: “Basta um de nós mudar de ideia e a decisão será totalmente modificada”. Considerando a situação apresentada e a proposição correspondente à afirmação feita, julgue o próximo item.

A negação da proposição pode ser corretamente expressa por “Basta um de nós não mudar de ideia ou a decisão não será totalmente modificada”.

Q03 (CESPE – 2017 – TRF 1ª Região) A partir da proposição P: “Quem pode mais, chora menos”, que corresponde a um ditado popular, julgue o próximo item.

Do ponto de vista da lógica sentencial, a proposição P é equivalente a “Se pode mais, o indivíduo chora menos”.

Q04 (AOCP – 2017 – Maringá PR) A afirmação “Se Pedro mente, então é segunda-feira” é logicamente equivalente à afirmação

(A) “Pedro mente todas as segundas-feiras”.
(B) “Se Pedro não mente, então não é segunda-feira”.
(C) “Se não é segunda-feira, então Pedro não mente”.
(D) “Pedro mente, ou é segunda-feira”.
(E) “Se não é segunda-feira, então Pedro mente”.

Q05 (FGV – 2017 – MPE BA) Considere a afirmativa:

“Tereza comprou pão e leite”.

Se a afirmativa acima é falsa, conclui-se logicamente que Tereza:

(A) não comprou pão nem leite.
(B) comprou pão, mas não comprou leite.
(C) comprou leite, mas não comprou pão.
(D) comprou pão ou comprou leite.
(E) não comprou pão ou não comprou leite.

Q06 (IBFC – 2017 –TJ PE) Considere a seguinte implicação lógica:

“Se é terça ou quarta, então trabalho e não vou ao cinema”.

Essa implicação é equivalente a:

(A) Se vou ao cinema e não trabalho, então não é terça, nem quarta.
(B) Se é terça ou não vou ao cinema, então trabalho ou é quarta.
(C) Se trabalho e não é terça, então vou ao cinema ou é quarta.
(D) Se vou ao cinema ou não trabalho, então não é terça, nem quarta.
(E) Se não trabalho ou não vou ao cinema, então não é terça, mas quarta.

Q07 (VUNESP – 2017 – TJ SP) Uma afirmação equivalente para “Se estou feliz, então passei no concurso” é:

(A) Se passei no concurso, então estou feliz.
(B) Se não passei no concurso, então não estou feliz.
(C) Não passei no concurso e não estou feliz.
(D) Estou feliz e passei no concurso.
(E) Passei no concurso e não estou feliz.

Q08 (FGV – 2017 – IBGE) Considere como verdadeira a seguinte sentença: “Se todas as flores são vermelhas, então o jardim é bonito”. É correto concluir que:

(A) se todas as flores não são vermelhas, então o jardim não é bonito;
(B) se uma flor é amarela, então o jardim não é bonito;
(C) se o jardim é bonito, então todas as flores são vermelhas;
(D) se o jardim não é bonito, então todas as flores não são vermelhas;
(E) se o jardim não é bonito, então pelo menos uma flor não é vermelha.

Q09 (IBFC – 2016 – EBSERH) A frase “O atleta venceu a corrida ou a prova foi cancelada” de acordo com a lógica proposicional é equivalente à frase:

(A) Se o atleta não venceu a corrida, então a prova foi cancelada.
(B) Se o atleta venceu a corrida, então a prova foi cancelada
(C) Se o atleta venceu a corrida, então a prova não foi cancelada
(D) Se o atleta não venceu a corrida, então a prova não foi cancelada
(E) Se a prova não foi cancelada, então o atleta não venceu a corrida

Q10 (CESPE – 2016 – ANVISA) A sentença Alberto é advogado, pois Bruno não é arquiteto é logicamente equivalente à sentença Bruno é arquiteto, pois Alberto não é advogado.

Q11 (IFBC – 2016 – EBSERH) A frase “Se a ave voa, então o sapo pula” é equivalente a frase:

(A) A ave não voa ou o sapo pula.
(B) O sapo não pula ou a ave voa.
(C) Se o sapo pula, então a ave não voa.
(D) O sapo pula se, e somente se, a ave voa.
(E) A ave não voa e o sapo não pula.

Q12 (IBFC – 2016 – EBSERH) De acordo com a lógica proposicional, a frase que é equivalente a: “Se Marcos estudou, então foi aprovado” é:

(A) Marcos não estudou e foi aprovado
(B) Marcos não estudou e não foi aprovado
(C) Marcos estudou ou não foi aprovado
(D) Marcos estudou se, e somente se, foi aprovado
(E) Marcos não estudou ou foi aprovado

Q13 (FUNCAB – 2016 – EMSERH) Dizer que “Alexandre foi aos Lençóis Maranhenses, se e somente se, fez sol” é logicamente equivalente dizer que:

(A) Não fez sol, se e somente se, Alexandre foi aos Lençóis Maranhenses.
(B) Se Alexandre foi aos Lençóis Maranhenses, então fez sol.
(C) Ou Alexandre foi aos Lençóis Maranhenses ou fez sol.
(D) Fez sol, se e somente se, Alexandre foi aos Lençóis Maranhenses.
(E) Se Alexandre foi aos Lençóis Maranhenses, então não fez sol.

Q14 (IADES – 2016 – CRESS-MG) Considerando duas proposições simples, p e q, a proposição ~p -> p é equivalente a

(A) ~p.
(B) p.
(C) ~ q.
(D) q.
(E) p ∧ q.

Q15 (VUNESP – 2016 – MPE SP) Uma afirmação equivalente à afirmação – Se Glória é dançarina ou cantora, mas não ambos, então Fábio não é ator. – é:

(A) Se Fábio não é ator, então Glória é dançarina ou cantora, mas não ambos.
(B) Se Fábio é ator, então Glória não é dançarina nem cantora ou Glória é dançarina e cantora.
(C) Se Fábio é ator, então Glória não é dançarina, mas é cantora.
(D) Se Glória não é dançarina nem cantora ou é dançarina e cantora, então Fábio é ator.
(E) Se Fábio não é ator, então Glória é dançarina, mas não é cantora ou Glória não é dançarina, mas é cantora.

Q16 (ESAF – 2016 – ANAC) A proposição “se o voo está atrasado, então o aeroporto está fechado para decolagens” é logicamente equivalente à proposição:

(A) o voo está atrasado e o aeroporto está fechado para decolagens.
(B) o voo não está atrasado e o aeroporto não está fechado para decolagens.
(C) o voo está atrasado, se e somente se, o aeroporto está fechado para decolagens.
(D) se o voo não está atrasado, então o aeroporto não está fechado para decolagens.
(E) o voo não está atrasado ou o aeroporto está fechado para decolagens.

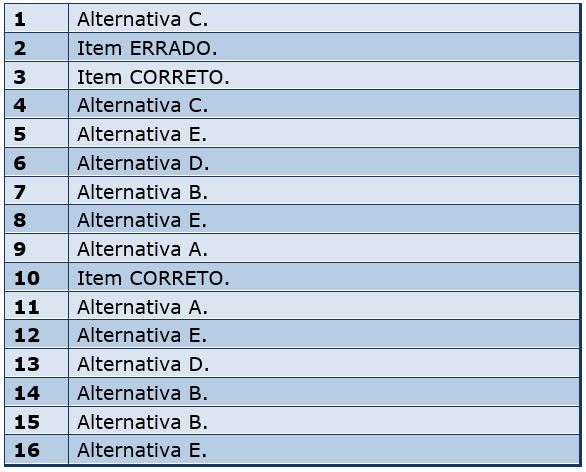
4. Gabarito

Enfim, chegamos ao final da nossa “breve” conversa sobre Equivalência Lógica.

Espero que tenham encontrado aqui dicas muito úteis.

Não estaria exagerando se dissesse que uma das questões de RML que você vai acertar no próximo concurso você aprendeu aqui.

Estamos aqui para te auxiliar: confiram minhas aulas demonstrativas de Matemática, Raciocínio Lógico, Estatística e Econometria na minha página no voceconcursado.com.br. Lá você vai encontrar as questões aqui propostas – sobre Equivalência Lógica – e muito mais.

Veja também: