STM – Análise da prova discursiva para o cargo 5
Meus caros amigos,
como foram de prova?
A prova discursiva para o “Cargo 5” do concurso do STM abordou, de forma conceitual, a definição de intervalo de credibilidade, tema pouco explorado em certames recentes (embora esteja indicado como objeto de avaliação do concurso). Vamos conversar um pouco sobre a questão:
(CESPE – 2018 – STM) A amostra aleatória simples X1, X2, …, Xn, retirada de uma distribuição de Bernoulli, é tal que
![]()
para x = 0 ou x = 1, 0 < p < 1 e k = 1, 2, …, n. O tamanho n da amostra é conhecido, e a probabilidade p representa o objeto de estimação, cuja estatística suficiente é dada pela soma
![]()
Considerando a situação hipotética acima apresentada, redija um texto dissertativo acerca de estimação por intervalos. Em seu texto, faça o que se pede a seguir:
- defina intervalo de credibilidade, e explique como ele pode ser interpretado; [valor: 14,00 pontos]
- exemplifique um intervalo de credibilidade; [valor: 12,00 pontos]
- discorra acerca das distinções entre um intervalo de credibilidade e um intervalo de confiança frequentista. [valor: 12,00 pontos]
Solução:
O conceito de “Intervalo de Credibilidade” está associado à Inferência Bayesiana, personificado no Teorema de Bayes, formulado por Thomas Bayes (1702 – 1761). O Teorema de Bayes foi inicialmente proposto para calcular probabilidades condicionais de eventos sujeitos às seguintes restrições:
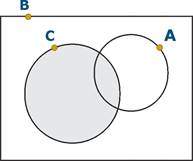
Algebricamente, escrevemos:
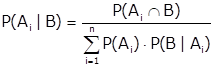
Após a morte de Bayes, seu trabalho caiu no esquecimento até que o matemático francês Pierre-Simon Laplace o redescobriu e, nas décadas de 1940-1950 trabalhou na reformulação do teorema de Bayes para ampliar sua aplicação. Essa reformulação teve como objetivo a substituição de eventos por variável aleatória.
![]()
Dito isto, podemos concluir que o Teorema de Bayes consiste na combinação da a priori com a informação proveniente dos dados amostrais, ou seja, combinar a distribuição a priori e a função de verossimilhança, originando a distribuição a posteriori, e tentar medir o grau de incerteza que se tem sobre a ocorrência de um determinado evento amostral.
Antes de continuar na trilha para definir “Intervalo de Credibilidade”, vamos apresentar dois novos conceitos: distribuição a priori e distribuição a posteriori:
- Distribuição a priori: representa a distribuição do parâmetro de interesse, independentemente dos dados amostrais observados. A distribuição a priori é o único elemento novo na análise bayesiana em relação à frequentista, distinguindo-as.
- Distribuição a posteriori: representa a distribuição do parâmetro de interesse, condicionalmente dos dados amostrais observados. Nessa distribuição, média, mediana e moda podem ser considerados potenciais estimadores pontuais.
No contexto da distribuição a posteriori, definimos o intervalo de credibilidade de forma probabilística como a pertinência ou não de θ ao intervalo. Isto não ocorre na inferência clássica para a interpretação do intervalo de confiança, que difere radicalmente. Ao calcular um intervalo de confiança de 95%, temos que se o experimento pudesse ser perfeitamente repetido inúmeras vezes, aproximadamente 95% dos inúmeros intervalos de confiança calculados conteriam o parâmetro de interesse mais desconhecido (θ). Já no caso da abordagem bayesiana, o intervalo de credibilidade de 95% para θ é o intervalo delimitado pelos percentis θ2,5% e θ97,5% da distribuição posterior p(θ|Y) para θ (Kinas e Andrade, 2010).

Matematicamente, um intervalo de credibilidade “C” de 100(1 – a)%, ou nível de credibilidade (ou confiança) 1 – a (alfa), para q (tetha) se
![]()
Exemplo:
Suponha que o intervalo de credibilidade de 90% para o parâmetro t seja [40 – 50]. Essa afirmação significa que a probabilidade a posteriori de que t esteja no referido intervalo é 0,90. Normalmente, os intervalos de credibilidade (bayesianos) não coincidem com os intervalos de confiança (freqüentistas) uma vez que o intervalo de credibilidade incorpora informação contextual específica do problema da distribuição a priori; por outro lado, os intervalos de confiança são baseados unicamente nos dados.
Agora, considerando intervalo de confiança de 90% na mesma faixa considerada acima e um grande número de amostras repetidas. 90% dos intervalos de confiança determinados incluirão o verdadeiro valor do parâmetro.



