Os assuntos mais cobrados pela FCC em Raciocínio Lógico
Conhecendo as operações básicas envolvendo frações e um pouco de leitura e interpretação de textos, a questão que acabamos de resolver se torna fácil e pode servir de base para muitas outras questões. Para a próxima questão, vamos destacar um dos principais modos que a FCC vem explorando questões do tema Proporção:
Questão 02:
(FCC – 2017 – TRT – 24ª Região – Técnico Judiciário – Área) Uma corda será dividida em três pedaços de comprimentos diretamente proporcionais a 3, 5 e 7. Feita a divisão, verificou-se que o maior pedaço ficou com 1 metro a mais do que deveria ser o correto para a medida do maior pedaço, e que o menor pedaço ficou com 1 metro a menos do que deveria ser o correto para a medida do menor pedaço. Se o único pedaço que saiu na medida correta ficou com 12 metros de comprimento, o menor dos três pedaços saiu com comprimento, em metros, igual a
(A) 8,6
(B) 7,5
(C) 6,2
(D) 4,8
(E) 5,6
Solução:
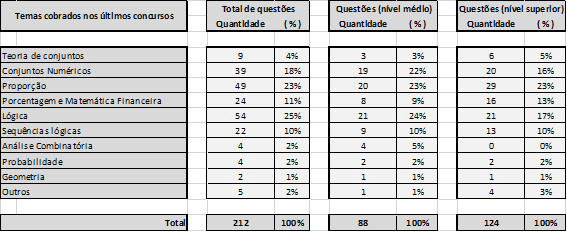
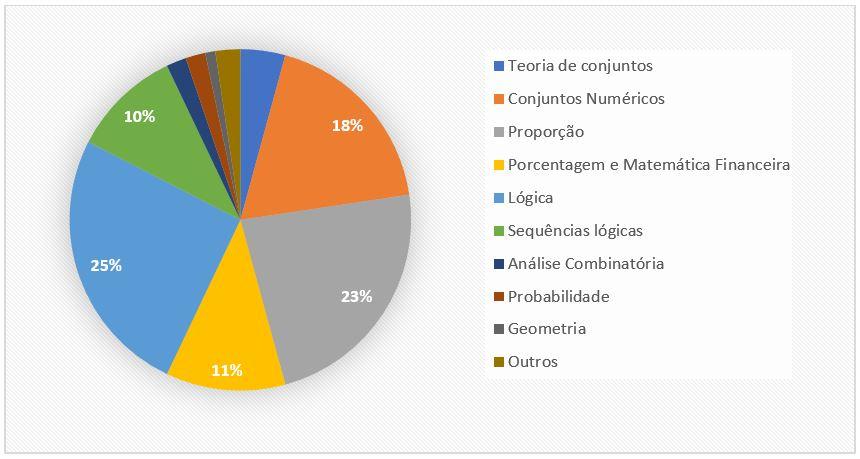
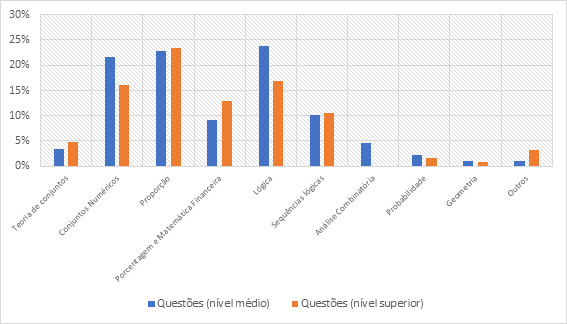
O conceito de proporção é de extrema importância para a maior parte das organizadoras, especialmente para a FCC e esteve presente em 23% das questões analisadas. Para resolver esta questão, vamos trocar algumas palavras sobre grandezas ou conjuntos diretamente proporcionais.
Dizemos que duas grandezas são diretamente proporcionais quando a razão entre elas é sempre constante. Consequentemente, o aumento (ou redução) de uma implica no aumento (ou redução) da outra na mesma proporção. Algebricamente, sendo k uma constante, podemos escrever:
![]()
Multiplicando a equação obtida por x, escrevemos y = kx e concluímos que grandezas diretamente proporcionais possuem como representação gráfica uma reta crescente que contém a origem do plano cartesiano.
Assim, como os comprimentos dos pedaços são proporcionais a 3, a 5 e a 7, podemos afirmar que existe a constante de proporcional k para a qual essas partes podem ser indicadas por 3k, 5k e 7k. Desses, o maior é 7k, o menor é 3k e 5k tem comprimento igual a 12 metros.
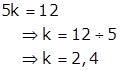
Ou seja, a constante de proporcionalidade (k) é igual a 2,4. Substituindo esse valor em 3k, 5k e 7k, determinamos os comprimentos de cada pedaço:
Porém, o menor pedaço (que deveria ter 7,2 metros) ficou 1 metro menor. Subtraindo 1 m de 7,2 m obtemos:
![]()
Gabarito: Alternativa C.
Enfim chegamos ao tema mais cobrado pela FCC e que não pode ser deixado de fora de qualquer revisão: Lógica Proposicional e, para conversar sobre este assunto, proponho uma questão que aborda a proposição condicional. A estrutura condicional, também chamada de implicação, é uma proposição lógica composta na qual as proposições que a compõe, P e Q, se apresentam na forma Se P então Q, representada simbolicamente por P -> Q.
![]()
Existe uma única possibilidade para que a implicação P -> Q seja falsa: P ser verdadeira e Q ser falsa. Nos demais casos, P -> Q é verdadeira. Essas informações estão consolidadas na seguinte tabela-verdade:
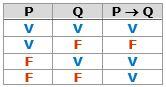
Em uma condicional P -> Q, dizemos que P é uma condição suficiente para Q e que Q é uma condição necessária para P. Ou seja, a não ocorrência de Q implica na não ocorrência de P.

- Existem duas equivalências muito importantes para a proposição condicional P -> Q que são muito utilizadas em questões que envolvem argumentos e implicações. Lembre com carinho delas:
P -> Q é equivalente a ~P ou Q
e
P-> Q é equivalente a ~Q -> ~P
- Existem duas equivalências muito importantes para a proposição condicional P -> Q que são muito utilizadas em questões que envolvem argumentos e implicações. Lembre com carinho delas:
- A negação da proposição condicional pode ser deduzida a partir da 2ª linha da tabela verdade da condicional, na qual o antecedente é mantido e consequente é negado. Enfim, a negação de P -> Q é:
P e ~Q
Após esclarecimento de alguns pontos sobre a estrutura condicional, vamos para a próxima questão:
Questão 03:
(FCC – 2016 – METRÔ-SP – Engenheiro Segurança do Trabalho) Considere as afirmações verdadeiras:
- Se chove, então o nível do rio sobe.
- Se o nível do rio não sobe, então dá para pescar.
- Se o nível do rio sobe, então dá para saltar da ponte.
- Não deu para saltar da ponte.
A partir dessas afirmações é correto concluir que
(A) o nível do rio subiu.
(B) não saltei da ponte porque é perigoso.
(C) não choveu e o nível do rio subiu.
(D) deu para pescar.
(E) choveu.
Solução:
Questão tradicional que envolve análise de proposições lógicas, mais precisamente, da proposição condicional e nossa tarefa resume-se a identificar conclusões a partir da informação de todas as proposições (simples e compostas) dadas são verdadeiras.
Uma estratégia que considero muito valiosa nestas questões está em usar o silogismo hipotético no qual dispomos duas (ou mais) condicionais de forma que o consequente de uma seja o antecedente da outra. Ou seja:
![]()
Assim, a ocorrência de P nos leva a concluir que R também ocorrerá. Dito isto, vamos começar nossa análise pela 4ª proposição (e que está na forma da negação de uma proposição simples). Sem levar em consideração a negação, consideraremos P4: Deu para saltar da ponte:
![]()
A seguir, vamos analisar a 3ª proposição, na qual o consequente é P4:“Deu para saltar da ponte”. Para obter uma conclusão válida, vamos utilizar, para III, a importante propriedade da contra positiva na qual partimos da negação do consequente e chegamos à negação do antecedente. Portanto, a proposição P3 -> P4: “Se o nível do rio sobe, então dá para saltar da ponte” é equivalente a:
![]()
De ~P4 e ~P4 -> ~P3 concluímos que “O nível do rio não sobe”. Perceba que podemos eliminar as alternativas A e C.

Analisaremos agora, a proposição I. Já sabemos que “o nível do rio não sobe”. Assim, observamos que o consequente da afirmação I: “Se chove, então o nível do rio sobe” é falso.

Para que a condicional de consequente falso seja verdadeira, o antecedente deve ser falso (veja a última linha da tabela verdade de P -> Q. Diante dessa informação, a proposição “chove” deve ser falsa. Ou seja, “não choveu” e podemos eliminar a alternativa E.
Por fim, utilizaremos ~P4 -> ~P3 e a proposição II para concluir que “Dá para pescar”.

Concluindo, foram três as conclusões obtidas a partir das informações apresentadas: (1) “O nível do rio não sobe”, (2) “não choveu” e (3) “dá para pescar”.
Gabarito: Alternativa D.
E então, já não sente que sua preparação foi levada ao próximo nível com esses poucos minutos? Imagine o que acontecerá quando você conferir minhas aulas demonstrativas:







Muito bom!
Parabéns! Artigo muito bem estruturado, bem sintetizado, de ótimos recursos visuais, facilitando a memorização e, por assim dizer, o aprendizado.
Sthephano, obrigado pelo comentário e pelas palavras de elogio. Seu retorno é muito importante: obrigado…
Muito Bom ! Seria bom se tivesse mais questoes com as soluçoes. Parabens e sucesso.
Gustavo, obrigado pelas palavras. Você pode encontrar mais questões comentadas nos artigos escritos e nos e-books lançados (https://voceconcursado.com.br/e-books-modo-hard/).
Fiquei Muito Interessado pelo seu post.Vou acompanhar seu Blog que é muito bom. É TOP ! Esse tipo de conteúdo tem me agregado muito conhecimento.Grato !
Excelente artigo! Que sua bondade e competência sejam recompensadas com muito sucesso!