Resolução da prova de Raciocínio Lógico Analista do TRT 7 e Gabarito Extraoficial
Vamos direto à resolução da prova:
Questão 25:
(CESPE – 2017 – TRT 7ª Região) Considere a proposição P:
A empresa alegou ter pago suas obrigações previdenciárias mas não apresentou os comprovantes de pagamento; o juiz julgou, pois, procedente a ação movida pelo ex-empregado.
A quantidade mínima de linhas necessárias para representar todas as combinações possíveis para os valores lógicos das proposições simples que compõem a proposição P é igual a:
a) 4
b) 8
c) 16
d) 32
Solução:
Considerando uma proposição composta formada com n proposições simples, o número de combinações de valores que cada uma das proposições simples p1, p2, p3, …, pn pode ter é
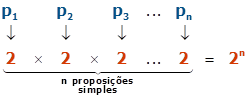
 |
O número de linhas da tabela-verdade de uma proposição composta formada por n proposições simples é 2n. |
A proposição apresentada pode ser representada por uma estrutura condicional na qual o antecedente é formado por 2 (duas)< proposições simples e o consequente por 1 (uma) proposição simples. Portanto, como é em número de 3 (três) as proposições simples que compõem P, o número de linhas da tabela-verdade para representa-la é
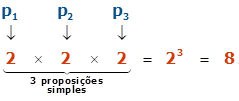
Gabarito: Alternativa B.
Questão 26:
(CESPE – 2017 – TRT 7ª Região) Assinale a opção que apresenta uma proposição equivalente, sob o ponto de vista da lógica sentencial, à proposição P:
“A empresa alegou ter pago suas obrigações previdenciárias mas não apresentou os comprovantes de pagamento; o juiz julgou, pois, procedente a ação movida pelo ex-empregado”.
a) A empresa alegou ter pago suas obrigações previdenciárias, mas não apresentou os comprovantes de pagamento, mas o juiz julgou procedente a ação movida pelo ex-empregado.
b) A empresa alegou ter pago suas obrigações previdenciárias, mas não apresentou os comprovantes de pagamento, ou o juiz julgou procedente a ação movida pelo ex-empregado.
c) Se o juiz julgou procedente a ação movida pelo ex-empregado, então a empresa alegou ter pago suas obrigações previdenciárias, mas não apresentou os comprovantes de pagamento.
d) Se a empresa alegou ter pago suas obrigações previdenciárias, mas não apresentou os comprovantes de pagamento então o juiz julgou procedente a ação movida pelo ex-empregado.
Solução:
A primeira vista, uma questão despretensiosa que nos pede para identificar qual o resultado da “tradução” da proposição P para a estrutura que usamos na lógica proposicional e, para fazê-lo, presentem atenção no termo que está destacado a seguir:
“A empresa alegou ter pago suas obrigações previdenciárias mas não apresentou os comprovantes de pagamento; o juiz julgou, pois, procedente a ação movida pelo ex-empregado”.
A palavra “pois” nos remete à ideia de consequência e pode ser substituída por “então”.
Gabarito: Alternativa E.
Questão 27:
(CESPE – 2017 – TRT 7ª Região)
Proposição Q: A empresa alegou ter pago suas obrigações previdenciárias, mas não apresentou os comprovantes de pagamento.
A negação da proposição pode ser expressa por:
a) A empresa alegou ter pago suas obrigações previdenciárias ou não apresentou os comprovantes de pagamento.
b) A empresa alegou ter pago suas obrigações previdenciárias e apresentou os comprovantes de pagamento.
c) A empresa não alegou ter pago suas obrigações previdenciárias nem apresentou os comprovantes de pagamento.
d) A empresa não alegou ter pago suas obrigações previdenciárias ou apresentou os comprovantes de pagamento.
Solução:
Esta é uma questão que envolve a negação da conjunção entre duas proposições lógicas simples e, para tal, vamos usar a importante Relação de De Morgan. Vamos começar analisando a proposição dada:
![]()
A ligação entre as proposições A e ~B se dá pelo uso do conectivo e (conjunção) e vamos determinar a negação desta proposição composta. Pelas relações de De Morgan, a negação da conjunção é equivalente à disjunção das negações, ou seja:
![]()
Ou seja, ![]() . Dito isto, concluímos que a negação da proposição Q é A empresa não alegou ter pago suas obrigações previdenciárias ou apresentou os comprovantes de pagamento.
. Dito isto, concluímos que a negação da proposição Q é A empresa não alegou ter pago suas obrigações previdenciárias ou apresentou os comprovantes de pagamento.
Gabarito: Alternativa D.
Questão 28:
(CESPE – 2017 – TRT 7ª Região) Considere as premissas P1 e P2 e a conclusão C:
P1: Se eu assino o relatório, sou responsável por todo seu conteúdo, mesmo que tenha escrito apenas uma parte.
P2: Se sou responsável pelo relatório e surge um problema em seu conteúdo, sou demitido.
C: Logo, escrevo apenas uma parte do relatório, mas sou demitido.
A negação da proposição P2 pode ser corretamente escrita na forma:
a) Se não sou o responsável pelo relatório e não surge um problema em seu conteúdo, não sou demitido.
b) Sou responsável pelo relatório e surge um problema em seu conteúdo, mas não sou demitido.
c) Não sou responsável pelo relatório, nem surge um problema em seu conteúdo, mas sou demitido.
d) Se sou responsável pelo relatório e surge um problema em seu conteúdo, não sou demitido.
Solução:
Esta questão explora a negação da proposição condicional e, para fazê-lo, vamos lembrar de uma informação bem importante sobre esse tema:

Assim, para negar a condicional P2, mantemos seu antecedente (sou responsável pelo relatório e surge um problema em seu conteúdo) e negamos seu consequente (não sou demitido).
Gabarito: Alternativa B.
Questão 29:
(CESPE – 2017 – TRT 7ª Região) Considere as premissas P1 e P2 e a conclusão C:
P1: Se eu assino o relatório, sou responsável por todo seu conteúdo, mesmo que tenha escrito apenas uma parte.
P2: Se sou responsável pelo relatório e surge um problema em seu conteúdo, sou demitido.
C: Logo, escrevo apenas uma parte do relatório, mas sou demitido.
O argumento apresentado se tornaria válido do ponto de vista da lógica sentencial se, além das premissas P1 e P2, a ele fosse acrescentada a proposição:
a) Sou responsável apenas pela parte que escrevi do relatório.
b) Eu escrevo apenas uma parte do relatório, assino o relatório e surge um problema no conteúdo.
c) Se não escrevo nenhuma parte do relatório, não sou demitido.
d) Não sou demitido ou não escrevo uma parte do relatório.
Solução:
Um argumento é toda afirmação de que uma dada sequencia finita P1, P2, P3, …, Pn de proposições tem como consequência ou acarreta uma proposição final Q. Assim, dizemos que um argumento é válido se, e somente se a conclusão é verdadeira todas as vezes que as premissas forem verdadeiras. Vamos começar nossa análise pela conclusão:
C: Logo, escrevo apenas uma parte do relatório e sou demitido.
Para que C seja verdadeiro, as duas proposições simples que a compõem devem ser verdadeiras (conjunção) e essas informações devem ser deduzidas a partir das premissas.
Para associar as premissas P1 e P2, precisamos de elementos de ligação entre elas, ou seja, “Escrevo parte do relatório”, “Assino o relatório” e “Surge um problema”.
Gabarito: Alternativa B.
Questão 30:
(CESPE – 2017 – TRT 7ª Região) Se, na prova, em que cada questão tem quatro opções de resposta, um candidato escolher ao acaso uma única resposta para cada uma das quatro primeiras questões, então a probabilidade de ele acertar exatamente duas questões será igual a:
a) 1/2.
b) 9/16.
c) 27/128.
d) 9/256.
Solução:
O problema proposto pode ser enquadrado na distribuição binomial onde um evento (marcar uma alternativa em uma questão) é repetido uma quantidade finita de vezes para o qual conhecemos a probabilidade de acertar uma questão (1/4) e a probabilidade de errar uma questão (3/4).
Então:

Gabarito: Alternativa C.





Não entendi a resolução da 30 :(
Boa tarde Tarcisio,
a expressão proposta como solução pode ser deduzida assim, considerado a probabilidade de acertar uma questão é (1/4) e a de errar uma questão é (3/4):
1) fixe uma ordem de 2 acertos e 2 erros. Abaixo, calcularei a probabilidade de acertar as duas primeiras e errar as duas últimas.
(A)(A)(E)(E) – Probabilidade (1/4)*(1/4)*(3/4)*(3/4) = 9/256
2) No entanto, temos que levar em consideração todas as ordens de acertos e erros (como se fossem permutações de dois A’s e dois E’s). Para cada uma dessas permutações, a probabilidade de ocorrência também é 9/256. O número de permutações (com elementos repetidos) é
4! / (2! 2!) = 24 / 4 = 6
3) Multiplicando os valores acima, obtemos 6 * 9/256 = 3 * 9/128 = 27/128
Observação: No estudo de probabilidade, essa categoria de problema se enquadra no que chamamos de distribuição binomial.