Gabarito extraoficial de Raciocínio Lógico TJPE
A prova de raciocínio lógico matemático do concurso para analista e técnico do Tribunal de Justiça de Pernambuco, organizado pela IBFC, cobriu de forma geral todos os temas do edital, concentrando os objetos de avaliação em Lógica Proposicional e Sequências e Progressões.
| Questão | Tema |
| 01 | Lógica proposicional (equivalência) |
| 02 | Lógica proposicional (negação) |
| 03 | Lógica proposicional (equivalência) |
| 04 | Lógica de argumentação (estruturas lógicas) |
| 05 | Teoria de conjuntos (operações) |
| 06 | Sequências e progressões (PA e PG) |
| 07 | Sequências e progressões (Soma dos termos de uma PA) |
| 08 | Sequências e progressões (Soma dos termos de uma PG infinita) |
As questões formuladas foram bem clássicas e tradicionais em provas de RLM: nesse quesito a banca não inovou. Por outro lado, podemos perceber problemas relacionados à cobrança de itens não explícitos no edital (questão 04) e contextualizações (estão mais para falsas contextualizações) que originaram questões mal formuladas (questões 05 e 07).
De forma geral, foi uma prova relativamente simples, com nível intermediário de dificuldade com estruturas de questões que já foram abordadas pela IBFC e por outras bancas. Enfim, já falei demais. Vamos ao que interessa: gabarito extraoficial da prova do concurso do TJPE…
Resolução da prova de Raciocínio Lógico Analista e Técnico TJPE:
Questão 1
(IBFC – TJPE – 2017) As expressões E1: (p ∧ r) v (~p ∧ r) e E2: (q ∨ s) ∧ (~q ∨ s) são compostas pelas quatro proposições lógicas p, q, r e s. Os valores lógicos assumidos pela expressão E1 Ù E2 são os mesmos valores lógicos da expressão:
a) r ∨ s
b) ~r ∧ ~s
c) ~r ∨ s
d) r ∨ ~s
e) r ∧ s
Solução:
De acordo com o exposto, temos que determinar qual alternativa apresenta uma expressão equivalente a E1 ∧ E2 e existem diferentes estratégias para tal. Podemos fazê-lo a partir da construção de tabelas verdades ou a partir de equivalências elementares da lógica matemática. Para a expressão E1, temos:
| p | r | p ∧ r | ~ p ∧ r | (p ∧ r) v (~p ∧ r) |
| V | V | V | F | V |
| V | F | F | F | F |
| F | V | F | V | V |
| F | F | F | F | F |
Perceba que E1 apresentou os mesmos valores que r. Conclusão:
E1 = r. Pois bem, favemos o mesmo para E2, definida por (q ∨ s) ∧ (~q ∨ s):
| q | s | q ∨ s | ~ q ∨ s | (q ∨ s) ∧ (~q ∨ s) |
| V | V | V | V | V |
| V | F | V | F | F |
| F | V | V | V | V |
| F | F | F | V | F |
Da mesma forma que observamos para E1, também percebemos que E2 pode ser simplificada e o resultado obtido é E2 = s. Agora encontramos elementos suficientes para obter a equivalência procurada para E1 ∧ E2:
Gabarito: Alternativa E.
Questão 2
(IBFC – TJPE – 2017) Um assistente judiciário deve analisar processos cada qual com exatamente 150 laudas. Um processo é considerado analisado se, e somente se, um técnico tiver lido pelo menos 135 laudas. Em outras palavras, um processo não é considerado analisado se, e somente se:
a) no máximo 15 laudas não forem lidas
b)15 laudas não forem lidas
c) no máximo 134 laudas forem lidas
d) no mínimo 15 laudas forem lidas
e) 14 laudas não forem lidas
Solução:
Para definir “processo analisado”, o enunciado formulou proposição do tipo se, e somente se: “Um processo é considerado analisado se, e somente se, um técnico tiver lido pelo menos 135 laudas”. Podemos representa-la assim:
| P: | Um processo é considerado aprovado. |
| Q: | Um técnico tiver lido pelo menos 135 laudas (x ≥ 135). |
A tabela verdade da bi-condicional é apresentada a seguir:
| P | Q | P ↔ Q |
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
Portanto, para que um processo não seja considerado analisado (valor de P falso) e, mesmo assim a condicional seja verdadeira, devemos ter Q falso (última linha da tabela verdade). Ou seja, vamos considerar a negação de x ≥ 135. Esse assunto foi amplamente tratado na nossa aula de “Lógica Proposicional”, na qual estudamos, usando recursos gráficos, negação de desigualdades.
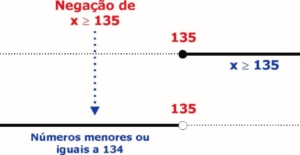
Gabarito: Alternativa C.
Questão 3
(IBFC – TJPE – 2017) Se p: o laudo foi elaborado e q: o parecer jurídico foi concluído, são duas proposições lógicas simples, então a proposição lógica: “Se o parecer jurídico não foi concluído, então o laudo foi elaborado” é falsa se, e somente se, a proposição:
a) p v q for verdade
b) ~q for verdade
c) p^q for falsa
d) p v q for falsa
e) p for falsa
Solução:
Outra questão que envolve equivalência lógica e para resolvê-la vamos usar lembrar de uma dica que apresentamos na nossa aula sobre lógica proposicional:
 |
A condicional P → Q é equivalente a ~P ∨ Q. |
Considerações iniciais feitas, vamos à análise de “Se o parecer jurídico não foi concluído, então o laudo foi elaborado” que, simbolicamente, pode ser representada por ~q → p. Transformando essa condicional em uma disjunção, temos:
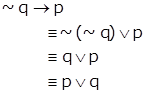
Portanto, ~q → p será falsa quando p ∨ q for falsa também.
Gabarito: Alternativa D.
Questão 4
(IBFC – TJPE – 2017) Os imóveis de Paula, Sheila e Carla são, não necessariamente nessa ordem, um apartamento, uma casa térrea e um sobrado. Um dos imóveis fica em São Paulo, outro em Minas e outro em Pernambuco. O imóvel de Paula é em São Paulo, o imóvel de Carla é um sobrado, o imóvel de Sheila não é em Minas e não é um apartamento. As cidades onde ficam o apartamento, a casa térrea e o sobrado, são respectivamente:
a) São Paulo, Minas e Pernambuco
b) São Paulo, Pernambuco e Minas
c) Pernambuco, Minas e São Paulo
d) Pernambuco, São Paulo e Minas
e) Minas, São Paulo e Pernambuco
Solução:
Para a resolução desta questão vamos construir uma tabela na qual veremos quais fatos apresentados são plausíveis no não. Traduzindo para nosso vocabulário de proposições, quais proposições (ou conjunção de proposições) são verdadeiras ou falsas.
| Apart. | Casa | Sobrado | SP | PE | MG | |||
| Paula | ||||||||
| Sheila | ||||||||
| Carla |
Começaremos com a afirmação: “o imóvel de Carla é um sobrado”. Na célula associada a Carla e sobrado colocaremos um V. Consequentemente Carla não é detentora do apartamento e não é detentora da casa térrea. Da mesma forma nem Paula e nem Sheila são proprietárias do sobrado.
| Apart. | Casa | Sobrado | SP | PE | MG | |||
| Paula | F | |||||||
| Sheila | F | |||||||
| Carla | F | F | V |
A seguir, usando as informações “O imóvel de Paula é em São Paulo, o imóvel de Sheila não é em Minas” concluímos que o imóvel de Sheila é em Pernambuco e o de Carla é em Minas Gerais.
| Apart. | Casa | Sobrado | SP | PE | MG | |||
| Paula | F | V | F | F | ||||
| Sheila | F | F | V | F | ||||
| Carla | F | F | V | F | F | V |
Para completar a tabela, vamos observar que “o imóvel de Sheila não é em Minas e não é um apartamento”. Ou seja, como o imóvel de Sheila não é um apartamento, só nos resta uma possibilidade: ser a casa.
| Apart. | Casa | Sobrado | SP | PE | MG | |||
| Paula | F | V | F | F | ||||
| Sheila | F | V | F | F | V | F | ||
| Carla | F | F | V | F | F | V |
Consequentemente, o imóvel de Paula é o apartamento.
| Apart. | Casa | Sobrado | SP | PE | MG | |||
| Paula | V | F | F | V | F | F | ||
| Sheila | F | V | F | F | V | F | ||
| Carla | F | F | V | F | F | V |
Portanto:
- O apartamento fica em São Paulo;
- A casa térrea fica em Pernambuco;
- O sobrado fica em Minas Gerais.
Gabarito: Alternativa B.
Questão 5
(IBFC – TJPE – 2017) Considere os conjuntos A = {0, 2, 3, 5, 6}; B = {2, 3, 5, 6, 9} e C = {0, 2, 4, 6}. Sabe-se que a soma de todos os elementos do conjunto [A ∩ (C – B)] representa o total de processos que necessitam de um parecer técnico. Nessas condições, o total de processos sem parecer técnico é:
a) 0
b) 8
c) 7
d) 11
e) 2
Solução:
Questão bem direta que envolve operações entre conjuntos. Para evitar errar um ponto fácil, todo cuidado para o parênteses que concedem prioridade para a expressão que está em seu interior. Pois bem, o conjunto C – B é formado por todos os elementos que pertencem a C e não pertencem a B:
C – B = {x / x ∈ A e x ∉ B}
Então, C – B = {0, 4} é formado retirando de C todos os elementos que também pertençam a B, ou seja, C Ç B. A seguir, determinamos a interseção desse conjunto com A:
A = {0, 2, 3, 5, 6}
C – B = {0, 4}
Repare que o único elemento comum é 0. Logo A ∩ (C – B) = {0}, ou seja, o número de processos sem parecer técnico é igual a zero.
Gabarito: Alternativa A.
Questão 6
(IBFC – TJPE – 2017) Considerando a sequência lógica 2, 3, 6, 6, 18, 12, 54, 24, … sabe-se que a diferença entre o décimo primeiro termo e o décimo segundo termo, nessa ordem, indica o total de vagas num concurso para analista judiciário. Nessas circunstâncias, se 500 candidatos passarem no concurso, o total desses candidatos que não preencherão as vagas será:
a) 362
b) 206
c) 62
d) 380
e) 110
Solução:
Normalmente, em questões que envolvem sequências ou padrões numéricos, começamos verificando se a mesma pode ser classificada como PA ou PG ou uma combinação da duas. A sequência apresentada,
2, 3, 6, 6, 18, 12, 54, 24, …
conforme nos ensina o saudoso professor Elon Lages (um dos expoentes do texto matemático brasileiro), pode ser desdobrada em duas subsequências, a partir dos termos de posição ímpar e de posição par.
Para os termos de posição ímpar (1º, 3º, 5º, 7º, …) temos uma PG de primeiro termo 2 e razão 3:
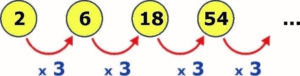
Os próximos dois termos dessa subsequência são:
- 54 x 3 = 162
- 162 x 3 = 486
Para os termos de posição par (2º, 4º, 6º, 8º, …) temos uma PG de primeiro termo 3 e razão 2:
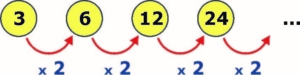
Os próximos dois termos da subsequência formada pelos termos de posição par são 48 e 96. Vejam porque:
- 24 x 2 = 48
- 48 x 2 = 96
Reagrupando esses termos, obtemos:
2, 3, 6, 6, 18, 12, 54, 24, 162, 48, 486, 96…
Por fim, os termos de posição 11 e 12 da sequência apresentada são 486 e 96. Logo, a diferença (subtração) entre eles é a11 – a12 = 486 – 96 = 390.
Gabarito: Alternativa E.
Questão 7
(IBFC – TJPE – 2017) Um assistente judiciário analisou, num primeiro dia de trabalho, 7 laudas de um processo com 785 laudas, num segundo dia analisou 3 laudas a mais do processo que no primeiro dia. Se a cada dia de trabalho esse assistente analisar 3 laudas a mais do processo que no dia anterior, então, após 15 dias de trabalho, o total de laudas do processo que ainda faltarão para serem analisados será igual a:
a) 420
b) 365
c) 295
d) 340
e) 435
Solução:
O número de laudas analisada por dia, 7, 10, 13, 16, 19… determina uma Progressão Aritmética (PA) de primeiro termo 7 e razão 3.
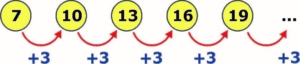
Para determinar o número de laudas que ainda faltarão para serem analisadas após 15 dias de trabalho precisamos, inicialmente, determinar quantas laudas foram analisadas até o 15º dia e, para tal, utilizaremos a fórmula da soma dos termos de uma PA:
![]()
Na fórmula, n corresponde à quantidade de termos que somaremos e, no contexto deste exercício, consideraremos n = 15. Porém, antes de determinar S15, determinaremos o 15º termo da sequência substituindo n = 15 em
![]()
Então:
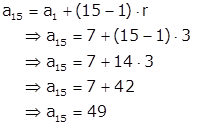
Substituindo esse resultado na fórmula da soma dos termos, encontramos:
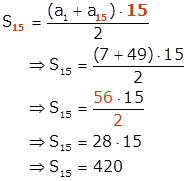
Ou seja, em 15 dias foram analisadas 420 laudas e, como o processo era formado por 785 laudas, o número de laudas que ainda serão analisadas é 785 – 420 = 365.
Gabarito: Alternativa B.
Questão 8
(IBFC – TJPE – 2017) Para acessar os dados de um arquivo um técnico judiciário deve saber o valor de x que é solução da equação x + x/2 + x/4 + … = 6. Nessas condições o valor de x deve ser:
a) 2
b) 1,5
c) 2,5
d) 3
e) 1
Solução:
O primeiro lado da igualdade corresponde à soma dos infinitos termos de uma PG de primeiro termo x e razão ½ (perceba que cada termo é igual à metade de seu antecessor). Usando a fórmula própria, temos:
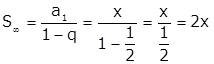
No entanto, como a soma é 6, temos:
![]()
Gabarito: Alternativa D.
Terminamos!
Espero que estas palavras, um tanto extensas, possam elucidar dificuldades e erros cometidos.
Abraço,
Professor Marcelo Eustáquio



