- Caracterize amostra aleatória simples e amostra estratificada, com técnicas probabilísticas.
- Caracterize amostra intencional e amostra por quotas, com técnicas não-probabilísticas.
- Apresente as vantagens e desvantagens do uso da amostragem probabilística em relação à amostragem não-probabilística nas pesquisas de opinião.
Ops! Esta questão ainda não tem padrão de resposta.
Ops! Esta questão ainda não tem resolução em texto.
Ops! Esta questão ainda não tem resolução em vídeo.
Questões Relacionadas
A tabela abaixo retrata a síntese das informações referentes ao consumo residencial de energia elétrica provenientes de duas amostras aleatórias de um total de 64 bairros selecionados. A amostra 1 é composta pelo consumo residencial de 30 bairros que foram selecionados dentro da região metropolitana de um Estado; os outros 34 bairros, todos localizados fora da região metropolitana do mesmo Estado, integram a amostra 2. Suponha que as amostras sejam oriundas de populações normais.
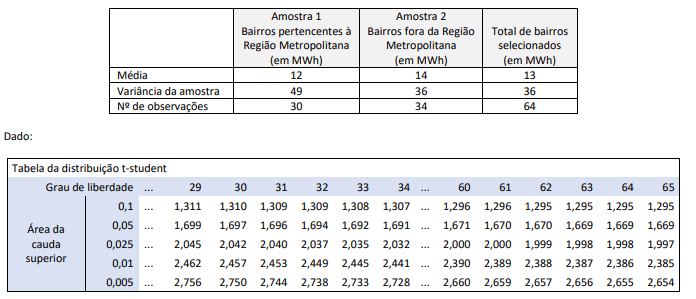
a) Considerando todos os bairros da amostra e a distribuição exata do estimador utilizado para estimar a média amostral, construa um intervalo bilateral de 95% de confiança para o consumo médio residencial de energ…
No âmbito de uma fiscalização na área de educação superior, uma equipe de auditoria precisou levantar informações sobre a renda média familiar dos alunos de uma Universidade Federal, relativas às seguintes áreas: biomédicas, tecnológicas e humanas. A equipe ficou na dúvida entre realizar um censo e uma amostragem. Por fim, acabou optando pela amostragem.
Com base na hipótese acima, elabore um texto dissertativo respondendo as seguintes perguntas:
- Apresente a diferença entre censo e amostragem. Cite 2 vantagens da utilização da amostragem.
- Descreva os passos necessários para a obtenção dos dados amostrais, justificando o plano amostral por você escolhido.
- Discuta como você compararia a renda…
A pandemia de COVID-19 evidenciou a importância da integração entre governo, instituições de pesquisa e setor produtivo. No Brasil, a Lei de Inovação (Lei nº 10.973/2004, alterada pela Lei nº 13.243/2016) permitiu a utilização de instrumentos como encomendas tecnológicas, transferência de tecnologia e compartilhamento de infraestrutura, viabilizando acordos entre institutos nacionais — como Fiocruz e Butantan — e farmacêuticas internacionais para a produção de vacinas em território nacional. Tal experiência revelou como a legislação pode contribuir para reduzir a dependência externa, garantir respostas rápidas a crises sanitárias e fortalecer a soberania científica e tecnológica do país.
Con…
