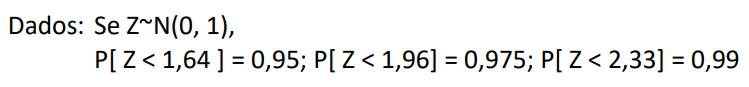Uma amostra aleatória simples de tamanho 400 foi obtida de uma densidade normalmente distribuída com média μμ e variância σ2σ2. Os dados das estatísticas suficientes foram:
x¯=43,4x¯=43,4 e ∑400i=1(xi−x¯)=3.591,0∑i=1400(xi−x¯)=3.591,0.
a) Estime um intervalo de 95% de confiança para μμ.
b) Teste, ao nível de significância de 5%, a hipótese nula de que μμ = 42,0 contra a hipótese alternativa de que μμ ≠ 42,0.
c) Determine o p-valor aproximado associado ao teste executado no item (b). Explique quais suposições você fez para obter o p-valor aproximado.
Ops! Esta questão ainda não tem padrão de resposta.
Ops! Esta questão ainda não tem resolução em texto.
Ops! Esta questão ainda não tem resolução em vídeo.
Questões Relacionadas
A Comissão de Valores Imobiliários (CVM), em auditoria realizada na empresa Y, avaliou a plausibilidade da justificativa apresentada na escolha da empresa X para conduzir uma oferta pública de ações. Após a realização do trabalho inicial, os inspetores identificaram o seguinte achado.
Achado: A equipe responsável pelo processo de seleção concluiu que a escolha pela empresa X se deve à eficiência de pelo menos 80% dos projetos de investimentos por ela conduzidos anteriormente. Para justificar esse fato, foi considerada uma pesquisa que apontou que apenas 9 entre 15 projetos de investimentos conduzidos pela empresa X obtiveram retornos positivos.
Considerando a situação hipotética precedente, …
A tabela abaixo retrata a síntese das informações referentes ao consumo residencial de energia elétrica provenientes de duas amostras aleatórias de um total de 64 bairros selecionados. A amostra 1 é composta pelo consumo residencial de 30 bairros que foram selecionados dentro da região metropolitana de um Estado; os outros 34 bairros, todos localizados fora da região metropolitana do mesmo Estado, integram a amostra 2. Suponha que as amostras sejam oriundas de populações normais.
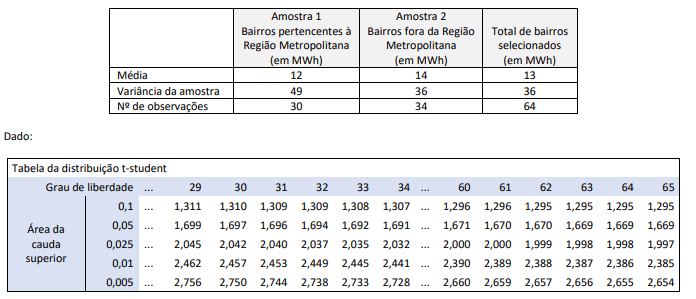
a) Considerando todos os bairros da amostra e a distribuição exata do estimador utilizado para estimar a média amostral, construa um intervalo bilateral de 95% de confiança para o consumo médio residencial de energ…
Suponha que uma amostra aleatória simples X1, X2, …, X625, de tamanho 625, de uma variável populacional suposta normalmente distribuída com média μ e variância σ² tenha apresentado os seguintes valores resumidos:
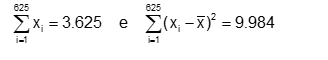
Deseja-se testar, ao nível de significância de 5% as hipóteses versus
a) Apresente o valor da média amostral e da variância amostral para esse conjunto de dados.
b) Apresente o critério de decisão a ser usado ao nível de significância de 5%.
c) Apresente a decisão a ser tomada com base nesses dados.
d) Calcule, aproximadamente, o p-valor associado a esses dados.
Dados:
- Z ~N (0, 1);
- P(Z < 1,64) = 0,95;
- P(Z < 1,96) = 0,975; e
- P(Z < 2,33) = 0,99.