Suponha que X1, X2, …, Xn seja uma amostra aleatória simples de tamanho n de uma variável populacional com distribuição Poisson parâmetro λ.
a) Mostre que a média amostral 𝑋̅ é o estimador de máxima verossimilhança de λ.
b) Lembrando que a média de uma distribuição Poisson (λ) é igual a λ, mostre que 𝑋̅ é um estimador não tendencioso de λ, ou seja, mostre que E[𝑋̅] = λ.
CONTEÚDO EXCLUSIVO
Confira nossos planos especiais de assinatura e desbloqueie agora!
CONTEÚDO EXCLUSIVO
Confira nossos planos especiais de assinatura e desbloqueie agora!
Ops! Esta questão ainda não tem resolução em vídeo.
Questões Relacionadas
A Comissão de Valores Imobiliários (CVM), em auditoria realizada na empresa Y, avaliou a plausibilidade da justificativa apresentada na escolha da empresa X para conduzir uma oferta pública de ações. Após a realização do trabalho inicial, os inspetores identificaram o seguinte achado.
Achado: A equipe responsável pelo processo de seleção concluiu que a escolha pela empresa X se deve à eficiência de pelo menos 80% dos projetos de investimentos por ela conduzidos anteriormente. Para justificar esse fato, foi considerada uma pesquisa que apontou que apenas 9 entre 15 projetos de investimentos conduzidos pela empresa X obtiveram retornos positivos.
Considerando a situação hipotética precedente, …
A tabela abaixo retrata a síntese das informações referentes ao consumo residencial de energia elétrica provenientes de duas amostras aleatórias de um total de 64 bairros selecionados. A amostra 1 é composta pelo consumo residencial de 30 bairros que foram selecionados dentro da região metropolitana de um Estado; os outros 34 bairros, todos localizados fora da região metropolitana do mesmo Estado, integram a amostra 2. Suponha que as amostras sejam oriundas de populações normais.
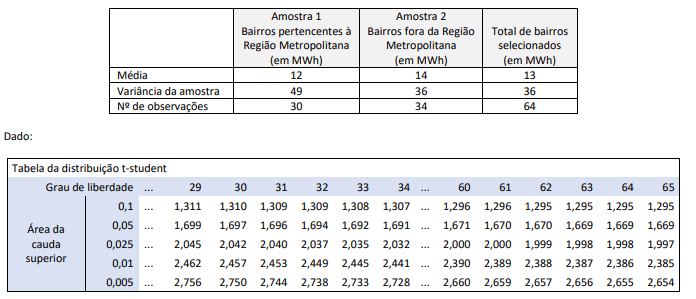
a) Considerando todos os bairros da amostra e a distribuição exata do estimador utilizado para estimar a média amostral, construa um intervalo bilateral de 95% de confiança para o consumo médio residencial de energ…
Para testar H0: μ ≤ 5 versus H1: μ > 5, em que μ é a média de uma variável aleatória populacional suposta normalmente distribuída, uma amostra aleatória simples de tamanho 256 foi observada e revelou os seguintes dados:
![]()
a) Apresente a estatística de teste a ser usada e o respectivo critério de decisão. Use α = 0,01.
b) Indique qual a decisão, com base nos dados apresentados.
c) Indique o p-valor aproximado associado.
d) Explique sucintamente qual aproximação do modelo teórico você precisou fazer.





Parabéns para quem conseguir enxergar as expressões matemáticas!
Só o estagiário conseguia ver mesmo. Obrigado pelo feedback.