Um quadriculado m × n com m linhas e n colunas, m, n ≥ 2, deve ser preenchido com números do conjunto {−1,0,1} de tal maneira que qualquer quadriculado 2 × 2 contido no quadriculado m × n tenha a soma de seus números igual a zero. Na figura abaixo tem-se um possível preenchimento de um quadriculado 2 × 3.
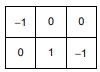
Seja S a soma de todos os números do quadriculado m × n.
a. Para m = 8 e n = 8, explique por que S = 0.
b. Considere o quadriculado 3 × 3 a seguir.
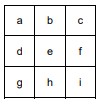
Verifique que S = a − e + i = c − e + g.
c. Para o quadriculado 5 × 5 sabendo-se apenas os valores da diagonal (a, b, c, d, e ∈ {−1,0,1}), como na figura abaixo, obtenha S.
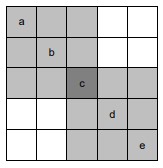
d. Determine o máximo de S para um quadriculado 5 × 5. Justifique sua resposta
Ops! Esta questão ainda não tem padrão de resposta.
Ops! Esta questão ainda não tem resolução em texto.
Ops! Esta questão ainda não tem resolução em vídeo.




