A tabela abaixo retrata a síntese das informações referentes ao consumo residencial de energia elétrica provenientes de duas amostras aleatórias de um total de 64 bairros selecionados. A amostra 1 é composta pelo consumo residencial de 30 bairros que foram selecionados dentro da região metropolitana de um Estado; os outros 34 bairros, todos localizados fora da região metropolitana do mesmo Estado, integram a amostra 2. Suponha que as amostras sejam oriundas de populações normais.
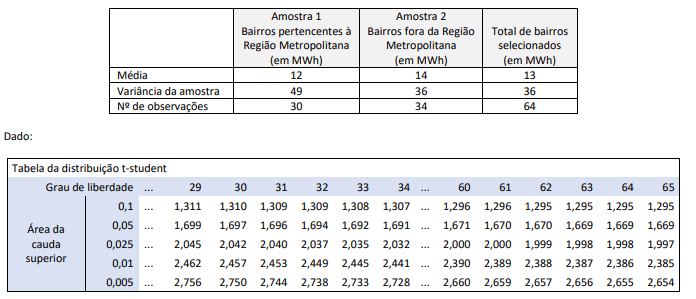
a) Considerando todos os bairros da amostra e a distribuição exata do estimador utilizado para estimar a média amostral, construa um intervalo bilateral de 95% de confiança para o consumo médio residencial de energia elétrica da população.
Para cada um dos itens b e c, formule as hipóteses, a estatística de teste, a distribuição correspondente sob H0, explicite o cálculo do valor observado, a regra de decisão e a decisão.
b) Considere, separadamente, as duas amostras indicadas na tabela acima. Teste, com 98% de confiança, a hipótese nula de que a razão das variâncias das duas populações seja 1 versus a hipótese de que as variâncias sejam diferentes de 1.
Dados:
𝑃𝑟𝑜𝑏(𝐹29;30 > 2,33) = 𝑃𝑟𝑜𝑏(𝐹30;29 > 2,381) = 0,01; 𝑠𝑒𝑛𝑑𝑜 𝐹~𝐹 𝑑𝑒 𝑆𝑛𝑒𝑑𝑒𝑐𝑜𝑟
𝑃𝑟𝑜𝑏(𝐹29;30 > 2,11) = 𝑃𝑟𝑜𝑏(𝐹30;29 > 2,144) = 0,02; 𝑠𝑒𝑛𝑑𝑜 𝐹~𝐹 𝑑𝑒 𝑆𝑛𝑒𝑑𝑒𝑐𝑜𝑟
c) Teste a hipótese de existir diferença entre os consumos médios residenciais das duas populações com 95% de confiança.
d) Que tipo de premissa, além da normalidade, foi necessária para resolver o item acima?
e) Como se denomina o menor nível de significância que leva à rejeição da hipótese nula nos testes de hipóteses?
CONTEÚDO EXCLUSIVO
Confira nossos planos especiais de assinatura e desbloqueie agora!
Ops! Esta questão ainda não tem resolução em texto.
Ops! Esta questão ainda não tem resolução em vídeo.
Questões Relacionadas
O município de Nova Esperança instituiu, em 2021, o Programa Municipal de Transferência de Renda Cidadã (PMTRC), voltado ao apoio de famílias em vulnerabilidade socioeconômica, com foco na redução da evasão escolar. Após dois anos de execução, a Secretaria Municipal de Desenvolvimento Social e a Secretaria de Educação decidiram realizar uma avaliação quantitativa do impacto do programa. O estudo, conduzido por uma equipe técnica da própria prefeitura, buscava identificar se o benefício financeiro havia contribuído significativamente para a permanência escolar e a melhoria dos indicadores de rendimento dos alunos beneficiados.
A equipe iniciou o processo com uma análise exploratória de dados …
Suponha que uma amostra aleatória simples X1, X2, …, X625, de tamanho 625, de uma variável populacional suposta normalmente distribuída com média μ e variância σ² tenha apresentado os seguintes valores resumidos:
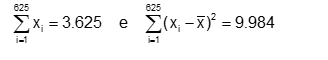
Deseja-se testar, ao nível de significância de 5% as hipóteses versus
a) Apresente o valor da média amostral e da variância amostral para esse conjunto de dados.
b) Apresente o critério de decisão a ser usado ao nível de significância de 5%.
c) Apresente a decisão a ser tomada com base nesses dados.
d) Calcule, aproximadamente, o p-valor associado a esses dados.
Dados:
- Z ~N (0, 1);
- P(Z < 1,64) = 0,95;
- P(Z < 1,96) = 0,975; e
- P(Z < 2,33) = 0,99.
O Índice de Desenvolvimento da Educação Básica (IDEB) é um dos principais indicadores de qualidade da educação no Brasil, considerando o desempenho dos alunos em exames padronizados e as taxas de aprovação. A análise dos resultados permite identificar problemas, propor políticas públicas e acompanhar a eficácia de estratégias educacionais.
Nos últimos três anos, uma escola pública de ensino médio de uma cidade de médio porte apresentou queda contínua no desempenho dos alunos em matemática. A direção escolar aponta como possíveis causas: metodologias de ensino pouco inovadoras, baixo tempo de estudo extraclasse, limitação no acesso a recursos digitais e condições socioeconômicas desfavoráveis…




