214914

Analise a situação hipotética a seguir.

Um estudo foi realizado com o objetivo de examinar os efeitos da inclusão de uma determinada dieta sobre o nível de colesterol dos indivíduos de uma região. Os participantes do estudo foram divididos aleatoriamente em dois grupos.

No primeiro grupo, denominado de “grupo de intervenção”, os indivíduos foram instruídos a seguirem a dieta, e no segundo grupo, denominado “grupo de controle”, os participantes não tiveram nenhuma mudança em suas dietas.

A variável de interesse é o nível sérico de colesterol (em mg/dL) medido oito semanas depois do início do estudo, que foi relacionado com as seguintes variáveis explicativas:

• GRUPO: grupo de intervenção (0 = controle, 1 = intervenção);

• NBC: nível baseline de colesterol medido no início do estudo (em mg/dL);

• IMC: índice de massa corpórea (em kg/m2);

• SEXO: sexo do participante (0 = mulher, 1 = homem).

Os coeficientes estimados e os erros-padrão das variáveis explicativas no modelo de regressão linear múltipla estão apresentados na tabela a seguir.

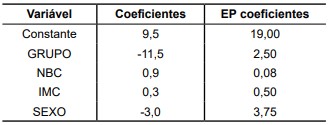
Resultados com valores ajustados para facilitar os cálculos.

A) Qual é a estimativa do nível sérico de colesterol após oito semanas de uma mulher do “grupo de intervenção” que tinha um nível baseline de colesterol igual a 240 mg/dL e um índice de massa corpórea de 30 kg/m²?

B) Supondo que o tamanho da amostra no estudo seja suficientemente grande para usar a aproximação normal, calcule um intervalo de confiança bilateral de 95% para o valor médio verdadeiro do nível baseline de colesterol (NBC). Interprete esse intervalo obtido dentro do contexto do problema.

Dado: Em uma curva normal padrão (Z), tem-se:

P(Z > 1) ≈ 0,16 ; P(Z > 1,65) ≈ 0,05

P(Z > 2) ≈ 0,025 ; P(Z > 3) ≈ 0,001