A tabela abaixo retrata a síntese das informações referentes ao consumo residencial de energia elétrica provenientes de duas amostras aleatórias de um total de 64 bairros selecionados. A amostra 1 é composta pelo consumo residencial de 30 bairros que foram selecionados dentro da região metropolitana de um Estado; os outros 34 bairros, todos localizados fora da região metropolitana do mesmo Estado, integram a amostra 2. Suponha que as amostras sejam oriundas de populações normais.
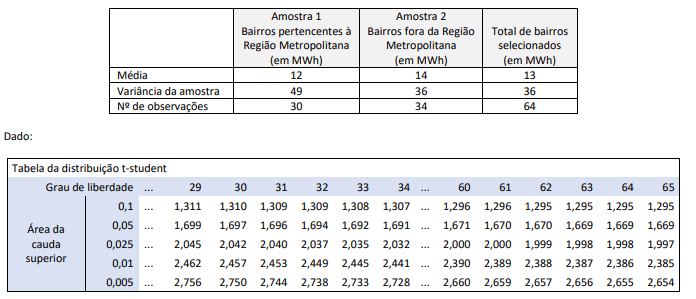
a) Considerando todos os bairros da amostra e a distribuição exata do estimador utilizado para estimar a média amostral, construa um intervalo bilateral de 95% de confiança para o consumo médio residencial de energia elétrica da população.
Para cada um dos itens b e c, formule as hipóteses, a estatística de teste, a distribuição correspondente sob H0, explicite o cálculo do valor observado, a regra de decisão e a decisão.
b) Considere, separadamente, as duas amostras indicadas na tabela acima. Teste, com 98% de confiança, a hipótese nula de que a razão das variâncias das duas populações seja 1 versus a hipótese de que as variâncias sejam diferentes de 1.
Dados:
𝑃𝑟𝑜𝑏(𝐹29;30 > 2,33) = 𝑃𝑟𝑜𝑏(𝐹30;29 > 2,381) = 0,01; 𝑠𝑒𝑛𝑑𝑜 𝐹~𝐹 𝑑𝑒 𝑆𝑛𝑒𝑑𝑒𝑐𝑜𝑟
𝑃𝑟𝑜𝑏(𝐹29;30 > 2,11) = 𝑃𝑟𝑜𝑏(𝐹30;29 > 2,144) = 0,02; 𝑠𝑒𝑛𝑑𝑜 𝐹~𝐹 𝑑𝑒 𝑆𝑛𝑒𝑑𝑒𝑐𝑜𝑟
c) Teste a hipótese de existir diferença entre os consumos médios residenciais das duas populações com 95% de confiança.
d) Que tipo de premissa, além da normalidade, foi necessária para resolver o item acima?
e) Como se denomina o menor nível de significância que leva à rejeição da hipótese nula nos testes de hipóteses?
CONTEÚDO EXCLUSIVO
Confira nossos planos especiais de assinatura e desbloqueie agora!
Ops! Esta questão ainda não tem resolução em texto.
Ops! Esta questão ainda não tem resolução em vídeo.
Questões Relacionadas
Com o intuito de estudar os determinantes do crédito concedido, , para a compra de um imóvel, foi proposto um Modelo de Regressão Linear Múltipla a partir da análise dos processos de clientes de uma instituição financeira, tendo especificado o seguinte modelo:
sendo que é o valor do crédito concedido, é o rendimento anual do cliente, é o valor de compra do imóvel, é a porcentagem das outras obrigações financeiras do cliente no seu rendimento (varia de 0 a 100) e é uma varável binária que assume valor 1, se o cliente tiver mais de 50 anos, e assume valor zero, caso contrário, e ln representa o logaritmo natural da variável.
Admita-se que foram verificadas todas as hipóteses do Mode…
O número de chamadas telefônicas, por minuto, que chegam ao serviço de atendimento ao consumidor de uma sociedade empresária segue uma distribuição de Poisson com valor esperado λ . Tendo por base a contagem do número de chamadas em 60 intervalos de um minuto, selecionados ao acaso, foram contabilizadas 120 chamadas.
a) Sabendo-se que λ=X é o estimador de máxima verossimilhança de λ , qual a estimativa de máxima verossimilhança para a probabilidade de não haver chamadas num minuto? Considere e¹=3.
b) Determine um intervalo de confiança bilateral, aproximado pela distribuição normal, de 95% para o número médio de chamadas por minuto.
c) Os funcionários do serviço de atendimento ao consumidor …
A pandemia de COVID-19 evidenciou a importância da integração entre governo, instituições de pesquisa e setor produtivo. No Brasil, a Lei de Inovação (Lei nº 10.973/2004, alterada pela Lei nº 13.243/2016) permitiu a utilização de instrumentos como encomendas tecnológicas, transferência de tecnologia e compartilhamento de infraestrutura, viabilizando acordos entre institutos nacionais — como Fiocruz e Butantan — e farmacêuticas internacionais para a produção de vacinas em território nacional. Tal experiência revelou como a legislação pode contribuir para reduzir a dependência externa, garantir respostas rápidas a crises sanitárias e fortalecer a soberania científica e tecnológica do país.
Con…




